As discussed in the previous chapter, a detailed wind assessment requires an extensive wind prospecting effort to collect a year or more of reliable wind data. Since such efforts are time consuming and expensive, it is advisable to first make a preliminary assessment based on available data. A preliminary assessment not only determines whether further effort is warranted, but also locates regions of significant potential for further study.
The full preliminary wind resource assessment for Eritrea, of which this thesis was a part, involved a number of parallel efforts to identify promising wind resource locations, including:
In the search for wind data, several potentially useful databases were found. Among them were direct surface observations, satellite derived wind data and assimilation products. The resolution (2-2.5 degrees) of the satellite derived wind data and assimilation products were insufficient for the purposes of this study. Therefore, this analysis uses only those data sets containing direct surface observations.
Four sources of direct surface wind information were found and analyzed: recent Eritrean station data, historical Italian station data, U.S. Air Force DATSAV2 surface records, and a climatic study of the Red Sea conducted by the U.S. Navy. These data sources are briefly described below. For detailed information on these and other databases investigated, see Appendix A.
Eritrean data (1994-1995). In 1994, the Eritrean Department of Water Resources began recording 15 minute wind speed averages at 7 stations located in towns and cities scattered throughout the highlands and western lowlands of Eritrea. Although less than one year of data was available for this study, rough (±1 m/s) mean annual wind speeds were estimated and are summarized in Table 5.
| Station |
|
|
|
| Asmera |
|
|
|
| Filfil |
|
|
|
| Kerkebet |
|
|
|
| Omhajer |
|
|
|
| Shambiko |
|
|
|
| Sh'eb |
|
|
|
| Tsorena |
|
|
|
Italian data (1930-1933). During the Italian occupation in the 1930's, daily average wind speeds were recorded at stations along the Italian-built railroad line from Mitsiwa'e to Keren in the Eritrean highlands. Mean annual wind speeds at four such stations are provided in Table 6.
| Station |
|
|
|
| Asmera |
|
|
|
| Faghena |
|
|
|
| Keren |
|
|
|
| Mitsiwa'e |
|
|
|
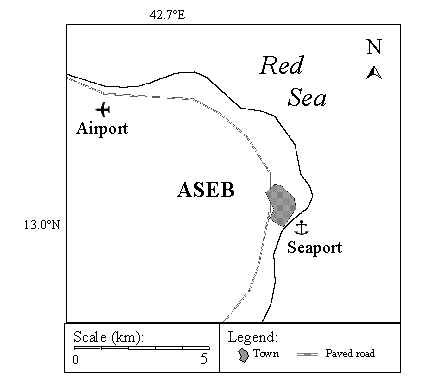
U.S. Air Force DATSAV2 data (1973-1992). Twenty years of DATSAV2 hourly meteorological records were available for several Eritrean cities, including Aseb (42º 43' E, 12º 58' N), for which a data set containing fourteen discontinuous years of observations (1977-80, 82-91) was obtained. The arithmetic mean of the 10-meter wind speeds in this data set indicated a mean annual wind speed of about 8 meters per second.
U.S. Navy Climatic Study of the Red Sea. A 1982 climatic study of the Red Sea conducted by Brower, Baldwin and Franks (1993) for the United States Navy mapped monthly mean wind speeds with 1 degree spatial resolution. For 7 of the 12 months (October through April), the report shows mean annual speeds of between 6 and 10 meters per second off the southern half of the Eritrean coastline. For the remaining months (May through September) the report indicates mean wind speeds of between 3 and 5 meters per second.
While these estimates suggest that wind resources in the highlands may be inadequate for utility-scale wind generation, one must keep in mind that the highland stations were not sited for wind prospecting purposes, and so are unlikely to have recorded the highest wind speeds in the region. Van Buskirk, Garbesi and Rosen (1997) argue that the channeling of wind through the hills and valleys of the highlands will create areas in which wind speeds are significantly enhanced. The Eritrean Department of Energy has been collecting additional wind data in the mountain passes near Asmera in an attempt to locate such sites. Estimates based on preliminary measurements indicate the existence of sites with mean annual wind speeds exceeding 5 meters per second.
Wind data obtained for Aseb and the Red Sea produced more promising results than did data for central Eritrea. The DATSAV2 data for Aseb indicated a mean annual wind speed of 8 meters per second, while the results of the Red Sea study by Brower, Baldwin and Franks (1993) indicated mean monthly wind speeds as high as 10 meters per second just off the southern coast. Although electricity demand in Eritrea is greatest in the central highlands, a more detailed study of winds in the Aseb area was conducted because of the high wind speeds recorded there. Analyses of winds at two Aseb sites and of winds over the Red Sea are presented below.
This study analyzes the DATSAV2 hourly data for Aseb to provide the following estimates for two sites at Aseb:

Data
The DATSAV2 data for Aseb consists of weather observations recorded by the Eritrean Civil Aviation Department. Wind speed values are human estimates calibrated to the standard 10 meter height, reported to the nearest meter per second. Until the end of Ethiopian occupation in 1991, observations recorded every 3 hours were archived by the United States Air Force Environmental Technical Application Center (USAFETAC) in the DATSAV2 Surface Database. Observations reported before 1986 were taken at the Airport station, while observations reported after 1986 were taken at the Seaport station.
The National Climatic Data Center (NCDC) provided fourteen years (1977-80, 1982-91) of DATSAV2 surface observations for Aseb. Each yearly subset contained between 13% (367 records) and 42% (1229 records) of the possible number of discrete 3-hour observations. The database included date, time, position, wind speed, wind direction and other weather related observations (see Appendix A). After removing incomplete or otherwise inconsistent data records, over 5,000 observations remained for each station.
Division of Data. The DATSAV2 database was first divided into two subsets according to whether the observations were recorded at the Airport or the Seaport station. In addition, mean monthly wind speed and direction data presented in Brower, Baldwin and Franks (1993) were used to further divide each subset to correspond with the two monsoon seasons in Eritrea. From this point on, the five months from the beginning of May through the end of September will be referred to as the summer season, while the seven months from the beginning of October through the end of April will be referred to as the winter season.
The resulting four subsets were analyzed independently. A preliminary analysis of these four data subsets is presented in Table 7
|
|
|
|
|
|
| N of observations |
|
|
|
|
| Minimum |
|
|
|
|
| Maximum |
|
|
|
|
| Arithmetic mean |
|
|
|
|
| Variance |
|
|
|
|
| Standard deviation |
|
|
|
|
| Standard Error |
|
|
|
|
| Skewness |
|
|
|
|
| Kurtosis |
|
|
|
|
Although the number of observations did not differ significantly on a month to month basis, observations did vary on a daily basis. Midnight and early morning observations were comparatively few, and for the first eight years were practically non-existent. To compensate for the fact that more observations were made during the daytime when wind speeds are highest, the four data subsets were further divided into eight 3-hour bins. The resulting 32 data subsets were analyzed separately. Figure 6 illustrates the data divisions and the number of observations in each subset.
| Airport | Seaport | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| Summer |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| Winter |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Because records for late evening and early morning hours were not recorded on a regular basis until after the observation site was moved to the Seaport, some 3-hour Airport data bins did not have sufficient data for analysis (minimum N=30). Of the sixteen data subsets for the Airport, six contained insufficient data for analysis: 21:00, 00:00 and 03:00 for each season.
Analysis
To estimate the nature of the missing data, we assumed similar wind regimes at the two stations, as they are separated by only about 10 kilometers of relatively flat, open land. To provide rough estimates of the empty data bins at the Airport, seasonal 3-hour wind speed averages and Weibull parameters for each station were calculated and graphed to determine correlations between the sites. This analysis is described in detail in the following sections.
Calculation of mean wind speeds. To estimate the mean annual
wind speed at the Airport, it was necessary to approximate mean seasonal
wind speeds for the 21:00, 0:00 and 3:00 data subsets. First, mean values
were calculated for the Airport and Seaport data subsets that contained
sufficient data, i.e. the data subsets including 6:00 through 18:00. These
mean values were then graphed, with the mean seasonal 3-hour Airport wind
speeds as the x-coordinate, and the mean seasonal 3-hour Seaport wind speeds
as the y-coordinate. The resulting scatter plot is presented in Figure
7.
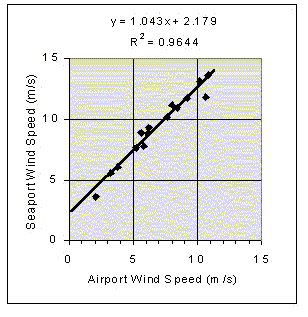
Using regression analysis, a linear correlation was derived between the time-correlated pairs of mean wind speeds at the two stations (R2 = 0.96) as shown in Figure 7. Each of the three missing values for the two seasons were then calculated as µa=m·µs+b, where µa and µs are the seasonal 3-hour mean wind speeds at the Airport and Seaport respectively, and m = 1.043, and b = 2.179 are the slope and y-intercept found in the regression analyses, respectively. The excellent correlation indicated by Figure 7 strongly supports the assumption that the Airport and Seaport stations have similar wind regimes.
Calculation of frequency distributions. To compensate for the uneven distribution of observations among the 3-hour bins, we planned to determine a frequency distribution for each subset, and then average the distributions to obtain the seasonal and annual wind speed frequency distributions for each site. As described above, however, some 3-hour subsets for the Airport station contained insufficient data to calculate the wind speed frequency distributions. To estimate these distributions, we planned to calculate Weibull parameters for the subsets with sufficient data, and then use them to estimate the Weibull parameters for the subsets with insufficient data. From these estimated parameters, model distributions for these subsets could then be constructed.
At this point it became clear that the wind speed database for Aseb contained an unusually high frequency of observations where the wind speed was zero (calms). This presented a problem because the standard Weibull distribution does not allow for a wind speed of zero. To resolve this problem, we employed a method described by Mulugetta and Drake (1996) in which a Weibull distribution is fit to the observed frequency distribution above zero meters per second, and calms are considered separately. This method tends to provide a more conservative estimate of mean wind speed by assuming that the reported frequency of calms is correct, whereas the standard Weibull distribution assumes that the frequency of calms is zero. This is particularly important in the case of the Aseb data, where the frequency of observed wind speeds commonly drops abruptly between zero and one meter per second, and then follows the expected Weibull distribution closely.
To the standard Weibull parameters of k and A is added a variable s denoting the frequency of calms. The equation of the non-cumulative, three-parameter Weibull
distribution then becomes:
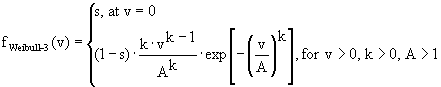 (18)
(18)such that f Weibull-3(v)·dv is the fraction of time the wind speed is in a bin centered at v, with bin size dv.
For each season, this three-parameter Weibull model was fit to the wind speed frequency distributions for the 13 subsets containing sufficient data. A best fit was obtained by minimizing the sum of the squared differences between points on the observed frequency distribution and the Weibull distribution.
The three-parameters of k, A, and s were calculated for each subset. To determine correlations between the parameters at the two stations, points with the Airport parameters as the x-coordinate and the Seaport parameters as the y-coordinate were plotted as shown in Figure 8.
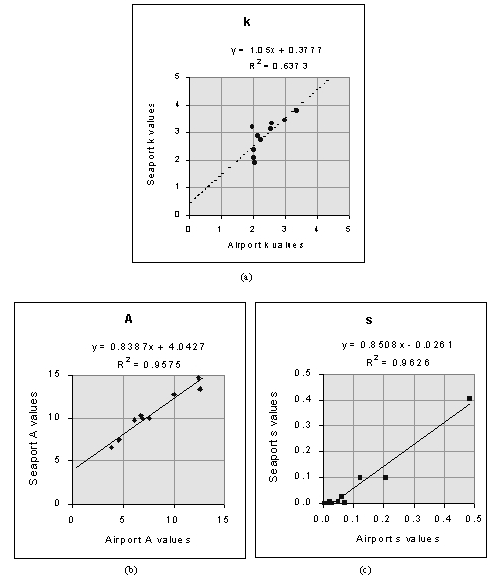
As can be seen in Figure 8(a), the scatter plot of the k parameters found at the Aseb Airport and Seaport did not indicate a particularly good correlation. Therefore the seasonal averages of the k values at the Airport were used as the k values of the empty bins. For both A and s, acceptable linear correlations were determined between the two stations. The missing values were then calculated as y = m·x + b, where y and x are the parameters at the Airport and Seaport respectively, and m and b are the slopes and y-intercepts found in the regression analyses.
According to the three-parameter method, mean wind speeds can be calculated as (Mulugetta and Drake 1996):
Seasonal wind speed frequency distributions for the Airport were calculated as the mean of the five observed and three estimated frequency distributions for each season. Seasonal wind speed frequency distributions at the Seaport were calculated as the mean of the eight observed frequency distributions.
Since the data were originally divided into a summer season of five months and a winter season of seven, annual distributions for each station were calculated as:
where fa(v) is the annual wind speed frequency distribution, and fs(v) and fw(v) are the summer and winter wind speed frequency distributions, respectively. To summarize the wind regime at the two Aseb sites, a best-fit three-parameter Weibull distribution to the non-cumulative annual wind speed distribution, fa(v), was determined for each site.
Calculation of capacity factors. The calculation of capacity factor for this study is based on the Flowind AWT-27 wind turbine, which has a rotor diameter of 27 meters and a rated capacity (Pr) of 250 to 300 kilowatts. The power curve, P(v), for the Flowind AWT-27 turbine is shown in Figure 9.
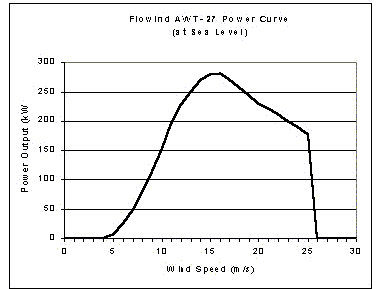
Wind power density, power output, and wind direction frequencies. Values for wind power density, potential power output and wind direction frequencies are calculated using Equations 15, 16 and 17, respectively.
An analysis of wind data over the Red Sea based on COADS is conducted as part of this study to provide seasonal and annual 0.1 degree resolution wind speed maps of the Red Sea. This is done to provide a reference against which qualitative estimates of wind potential along the southern Eritrean coastline can be derived based on the relationship between winds at Aseb and winds off the coast of Aseb.
Data
COADS is a global collection of instantaneous marine observations recorded between 1854 and 1993. The wind speed data recorded in COADS are based on the Beaufort scale, human estimates that relate marine surface roughness with wind speed. Wind speed records in the database are provided to the nearest knott.
COADS is available from the National Center for Atmospheric Research (NCAR) in Boulder, Colorado. An electronic data file containing the portion of COADS bounded by 12°N 32°E and 30°N 44°E, was received in two files: the Compressed Marine Reports (CMR) and the Long Marine Reports (LMR). These two data sets differ in both time period and format. The earlier set (CMR) covers the period 1854-1969. The later set (LMR) covers the period from 1969 to 1993.
Due to insufficient spatial resolution in early observations, this analysis will utilize COADS data beginning in 1940. Until the 1930's, the majority of observations were reported to the nearest 1.0 degree. All observations recorded after 1940 were reported to the nearest 0.1 degree. After removing pre-1940 records and records with missing data, the database contained a combined total of over 650,000 observations.
Analysis
To compensate for uneven temporal sampling in the data set, the combined
CMR/LMR database was divided into seasonal 6-hour bins, resulting in 8
data subsets. Mean wind speeds were calculated only for positions containing
data in all 8 data subsets. For each of the 8 temporal data subsets, the
arithmetic average of wind speeds in each 0.1 degree bin was calculated.
The arithmetic averages of corresponding bins in the 4 winter and 4 summer
data subsets were calculated to estimate seasonal wind speeds. For each
corresponding bin in the two seasonal subsets, mean annual wind speeds
were calculated as the sum of 5/12 the summer average and 7/12 the winter
average.