The results of the analysis described in Chapter 5 are presented below.
Results presented here represent wind speed values at 10 meters height; however, it is expected that wind speeds at typical turbine hub heights of 30 meters or more would be higher than those presented here (see Vertical estimation of wind speed using the power-law model in Chapter 3).
Table 8 summarizes the results of the analysis of DATSAV2 wind speed data. Values presented in Table 8 were calculated from observed wind speed data, with the exception of 21:00, 0:00 and 3:00 at the Airport. These values, printed in italics, were estimated as described in Chapter 5.
Table 8. Results of the analysis of DATSAV2 data, showing mean seasonal and annual 10-meter wind speeds (in m/s) for 3-hour periods at the Aseb stations.
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 9 shows the parameters obtained using three-parameter Weibull fits to the observed seasonal 3-hour wind speed distributions as described in Calculation of Frequency Distributions in Chapter 5. Again, values for 21:00, 0:00 and 3:00 are estimated as described in Chapter 5. Mean wind speeds presented in Table 9 are based on Equation 19.
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
The majority of mean seasonal 3-hour wind speed values estimated using the three-parameter Weibull method (Table 9) are within 2 percent of observed mean wind speeds (Table 8). The greatest difference between calculated values and observed values was 3.3 percent at 0:00 at the Seaport.
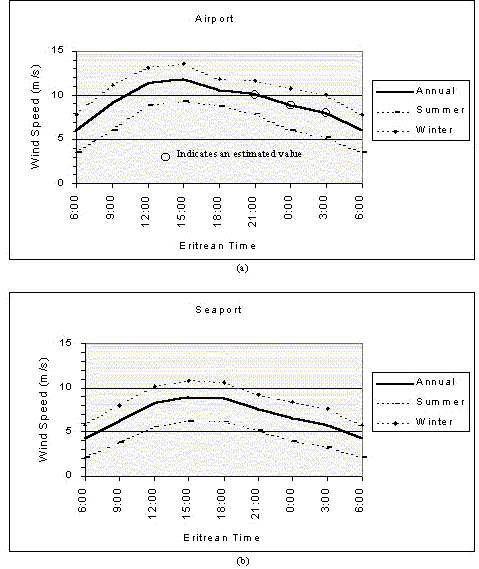
Figure 10 shows the mean diurnal wind speed variations at the Aseb stations. The higher wind speeds indicated at midday would increase power supplies during the peak demand period. Here, again, it is clear that the wind speeds at the two stations are closely related.
Figure 11 shows the three-parameter Weibull fits to the annual wind speed distributions at the two Aseb stations. In Figure 11(a), the "Observed" distribution at the Airport is the average of the 5 observed distributions and 3 predicted distributions as described in Chapter 5. The "Observed" distribution in Figure 11(b) is the arithmetic average of the 8 observed 3-hour distributions at the Seaport.

Figure 10. Graphs showing mean diurnal wind speed
variations at the Aseb stations
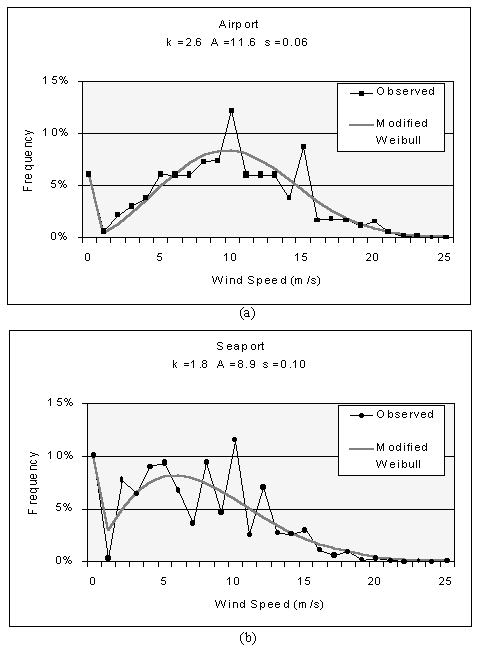
Figure 11. A graph showing three-parameter a Weibull fit to the observed annual wind speed distributions at the Aseb Airport.
Figure 12 shows mean annual wind speeds in the Red Sea along the southern Eritrean coastline. According to these results, mean annual wind speeds over the southern Red Sea are in excess of 6 meters per second for about two hundred kilometers of the lower Eritrean coast. This suggests that wind sites with high wind power potential may be found along the entire length of the southern Eritrean coastline.
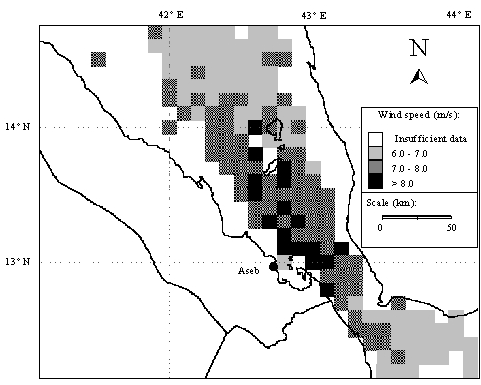
Figure 12. Map showing mean annual wind speeds along the southern Eritrean coastline
Table 10 shows the estimated wind power densities, capacity factors,
and projected energy output values calculated for the two Aseb stations.
The calculations presented in Table 10 use the following assumptions:
| Rotor diameter D: | 20 meters |
| Average turbine spacing: | 10D x 5D |
| Array and system efficiency: | 75% |
|
|
|
|||
|
|
|
|
|
|
| Mean Annual Wind Speed (m/s) |
|
|
|
|
| Mean Annual Wind Power Density (W/m2) |
|
|
|
|
| Capacity Factor (%) |
|
|
|
|
| Wind Power available per turbine (kW) |
|
|
||
| Electrical Power generated per turbine (kW) |
|
|
||
| Annual Energy Output per turbine (GWh) |
|
|
||
| Annual Energy Output per kilometer (GWh/km) |
|
|
||
These values indicate that both stations qualify for the highest wind power class of 7.
A typical annual average wind power density for utility scale energy
production is 450 W/m² at turbine hub height (Cavallo, Hock and Smith
1993). The wind power densities shown in Table 10 are high because of the
very high wind speeds during the winter months at Aseb. It should be noted,
however, that the wind power supply between May and September is expected
to be considerably lower.
Figure 13 shows seasonal wind roses based on the analysis of DATSAV2 data for the two Aseb stations.
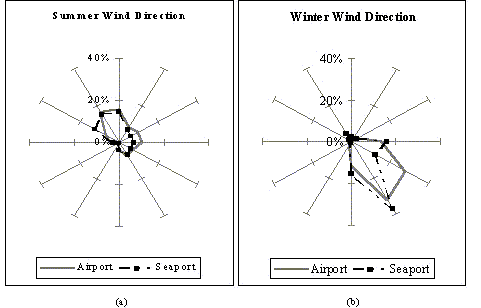
Figure 13. Wind roses showing wind direction frequency distributions during the summer and winter monsoon seasons at Aseb
Once again, it can be seen that the winds at the two stations follow
each other very closely. It is also noteworthy that the strong winter winds
blow predominantly from the southeast. In areas with unidirectional or
bi-directional winds, more efficient wind turbine spacing may be possible
as turbines may be erected closely together in a line perpendicular to
the wind direction. As a result, the array efficiency of 75% assumed for
this analysis may be an underestimation.
Any resource assessment based on meteorological data is only suggestive and serves merely as an indicator of a promising resource. Such estimates cannot be used as the basis of economic calculations for utility-scale power generation without extensive site-specific monitoring. For example, consider a site with an estimated annual average wind speed of 6 ± 1 m/s, implying that the average annual wind speed might be anywhere between 5 and 7 m/s. This corresponds to a factor of 2.7 difference in power. An error this large can make the difference between a wind site that is economical for energy production and one that is not. At Aseb, however, the estimated mean annual wind speed of 9.5 meters per second would be economical even if this value is off by 1 or even 2 meters per second.
There are reasons to believe that a study such as this would underestimate the wind resources of an area. Wind monitoring stations are typically found in towns or cities. Since people do not normally choose to live in areas with extremely high wind speeds, it is likely that there are sites with better wind resources. In addition, regional studies, such as the one presented here, show only large areas of high wind resource potential. The preliminary study may not detect a mountain pass, within an otherwise low potential area, into which strong winds are regularly funneled. Such an area will likely be overlooked, even though it may be a very promising site.
Mathematical models may be the cause of inaccuracy. This is especially likely in regions such as Eritrea that have complex terrain (e.g. mountains) and wind flows (e.g. convective flows). Because mathematical models are less likely to be accurate when used such areas, this study utilized such models minimally. However, use of the 1/7 power law (see Wind Assessment in Chapter 3), which assumes relatively flat terrain, was necessary to estimate wind power potential at the expected turbine hub height. Although the Aseb Airport is located on a flat plain at only 14 meters elevation, there is still some chance that the estimated 30-meter values presented in this chapter overestimate the true potential.
Most wind speeds presented in this study are based on human estimates.
Although these estimates are given by experienced personnel, human estimates
may not be as accurate as modern equipment, such as anemometers with automatic
data loggers. In addition, wind speed values at the Aseb stations were
recorded to the nearest meter per second, with the result that each observation
had a possible error of ±0.5 meter per second. Due to conversion
from the Beaufort scale to knots to meters per second, wind speed estimates
for the Red Sea may be off by as much as 2 meters per second or more. However,
since the main focus of this study is Aseb, and the Red Sea analysis was
done only for comparison, higher accuracy for the Red Sea results is not
critical.