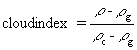
Remote sensing techniques can be applied to the estimation of renewable energy resources. This study uses these techniques to make preliminary estimates of biomass production, irradiance distributions and rainfall patterns. In the analysis of biomass production, there is no Eritrean ground data available, so we utilized correlations between tree leaves plus above ground biomass with NDVI which were produced for other Sahelian countries. The results show that Eritrea's biomass production for March, April, June, and July is about 0.58, 0.26, 0.77,and 0.99 millions metric tones with corresponding confidence interval of ±0.164, ±0.063, ±0.109, and ±0.131 millions metric tones respectively. The confidence interval associated with the result is about 28%, 24%, 14%, and 13% of the production for March, April, June, and July respectively.

For radiation mapping, images of the Meteosat satellite were used. The fact that clouds reflect more radiation compared to the earth surface feature will give rise to an inverse relationship between satellite pixel cloud index and clear sky index. By doing regression analysis between the difference of average and minimum images of the month with the ground radiometric values, irradiance distribution maps of Eritrea for 9am, 10am, 11am, 12am, 1pm, 2pm, and 3pm were produced. The average RMS error associated with the correlation is about 5%. Error due to the assumption that ground albedo is uniform will give rise to an additional 2% error. Besides there exist other errors due to neglect of ground data correction, atmospheric correction and geometrical correction which is estimated to be a few percent. Daily average radiation map was also produced by using regression analysis between cumulative solar radiation and average pixel of the radiation for the above mentioned hours of the month. The RMS error of the regression analysis is about 0.133 Kw-hr/m² which is about 2.5% of the average radiation.

For production of rainfall distribution maps, historical rainfall of over 20 years was used as there is no adequate and dependable current time data. The months of interest were January, February, and March. Following the regression analysis between the historical rainfall and Normalized Difference Vegetation Index (NDVI), rainfall distribution map was produced. Good correlation occurred for NDVI of a month with rainfall of previous months i.e., March NDVI vs. January Historical Rain, March NDVI vs. February rain, and April NDVI vs. March rain. The correlation coefficient for the above regression analysis are greater than 0.9.

TITLE PAGE
ABSTRACT
TABLE OF CONTENTS
LIST OF ILLUSTRATIONS
ACKNOWLEDGMENTS

1. INTRODUCTION
1.1     OBJECTIVE AND SCOPE
1.2     BACKGROUND ON REMOTE SENSING
1.2.1         REMOTE SENSING
1.2.2         HISTORICAL DEVELOPMENT OF REMOTE SENSING
1.3     SIGNIFICANCE OF REMOTELY SENSED BIOMASS ESTIMATES
1.4     SIGNIFICANCE OF RADIATION AND RAINFALL DISTRIBUTION MAPS
1.5     LITERATURE REVIEW
2. PRINCIPLES INVOLVED
2.1     SOURCES OF ELECTROMAGNETIC (EM)-RADIATION
2.2     ENERGY INTERACTION IN THE ATMOSPHERE
2.2.1         SCATTERING
2.2.2         ABSORPTION
2.3     ENERGY INTERACTION WITH THE EARTH'S SURFACE
2.4     DATA ACQUISITION AND INTERPRETATION
2.5     REMOTE SENSING OF BIOMASS PRODUCTION
2.5.1         REFLECTANCE CHARACTERISTICS OF GREEN PLANTS
2.5.2         PRINCIPLES OF DETECTION
2.5.3         ESTIMATION OF RADIATION USE EFFICIENCY IN PLANTS
2.6     REMOTE SENSING OF RADIATION INTENSITY
2.6.1         SOLAR CONSTANT
2.6.2         RADIATION REFLECTED AND RECEIVED BY THE GROUND
2.6.3         ATMOSPHERIC EFFECTS
2.6.3.1             AIR MASS RATIO
2.6.3.2             ATMOSPHERIC ABSORPTION ND REFLECTION
2.6.4         IRRADIANCE VARIATION
3. METHODOLOGY 
3.1     METHOD FOLLOWED FOR ESTIMATION OF BIOMASS PRODUCTION
3.1.1         PRODUCTION OF 10 DAY COMPOSITE IMAGES
3.1.2         PRODUCTION OF QUALITY IMAGES
3.1.3         PRODUCTION OF BIOMASS MAPS
3.1.4         ESTIMATION OF BIOMASS YIELD
3.2     METHOD FOLLOWED FOR PRODUCTION OF RADIATION MAPS
3.2.1         EXTRACTION OF QUALITY RAW IMAGES
3.2.2         PROCESSING OF RAW IMAGES
3.2.3         PROCESSING OF GROUND DATA
3.2.4         CORRELATION OF IMAGES WITH GROUND DATA
3.2.5         EXTRAPOLATION
3.2.6         PRODUCTION OF HOURLY RADIATION MAPS
3.2.7         PRODUCTION OF DAILY AVERAGE RADIATION FOR NOVEMBER
3.3     METHOD FOLLOWED FOR PRODUCTION OF RAINFALL MAPS
3.3.1         EXTRACTION OF NDVI VALUES
3.3.2         REGRESSION ANALYSIS
3.3.3         PRODUCTION OF RAINFALL DISTRIBUTIONS
4. RESULTS
4.1     RESULTS ON ESTIMATION OF BIOMASS PRODUCTION
4.2     RESULTS ON PRODUCTION OF RADIATION MAPPING
4.3     RESULTS ON PRODUCTION OF RAINFALL CORRELATIONS 
5. CONCLUSION

APPENDIX
BIBLIOGRAPHY

LIST OF ILLUSTRATIONS

FIGURE 1- SPECTRAL DISTRIBUTION OF EMITTED ENERGY FOR A BLACK BODY
FIGURE 2- RAYLEIGH'S SCATTERING
FIGURE 3- ATMOSPHERIC ABSORPTION
FIGURE 4- REFLECTANCE CHARACTERISTICS
FIGURE 5- VARIATION OF INTENSITY AT DIFFERENT LATITUDE
FIGURE 6- BIOMASS PRODUCTION FOR MARCH 1996
FIGURE 7- BIOMASS PRODUCTION FOR APRIL 1996
FIGURE 8- BIOMASS PRODUCTION FOR JUNE 1996
FIGURE 9- BIOMASS PRODUCTION FOR JULY 1996
FIGURE 10- ERITREA WITH GRID OF O.5 DEGREES
FIGURE 11- 9AM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 12- 10AM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 13- 11AM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 14- 12AM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 15- 1PM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 16- 2PM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 17- 3PM SOLAR IRRADIANCE FOR NOVEMBER 1995
FIGURE 18- DAILY AVERAGE RADIATION FOR NOVEMBER 1995
FIGURE 19- REGRESSION ANALYSIS FOR 11AM, NOVEMBER 1995 
FIGURE 20- REGRESSION ANALYSIS FOR 3PM, NOVEMBER 1995
FIGURE 21- REGRESSION ANALYSIS OF DAILY AVERAGE RADIATION, NOVEMBER 1995
FIGURE 22- HISTORICAL RAINFALL FOR JANUARY 50
FIGURE 23- HISTORICAL RAINFALL FOR FEBRUARY 51
FIGURE 24- HISTORICAL RAINFALL FOR MARCH 52
FIGURE 25- REGRESSION ANALYSIS FOR MARCH RAINFALL 53

ACKNOWLEDGEMENT

First of all, I am greatly indebted to my Advisor Dr.Robert Van Buskirk, for his unlimited dedication towards the work, ambition, enthusiasm, golden suggestions, resourcefulness that with out him this paper would not have been accomplished successfully.

Secondly, I like to thank the Ministry of Energy and Mines for letting me work in their research center, and providing me computers with important application software, essential satellite data and ground data to work with. In addition, I like to acknowledge the encouragement and assistance I received from the staff members of the research center while I was through the study.

Next I would like to aknowledge the Water Resources department for providing the radiation data that was used in the solar mapping work, and Daniel Yohannes for beginning the earliest Eritrean radiation maps in June 1996.

Last but not least, I like to convey my gratitude to the Physics Department, University of Asmara, for letting me work on this project and for providing me with full access to computers in editing the manuscript.
 

1. INTRODUCTION

1.1 OBJECTIVE AND SCOPE

The objective of this paper is to perform a preliminary analysis of the applicability of remote sensing techniques to biomass, radiation and rainfall estimation in Eritrea. For the estimation of biomass, as there is no ground data, satellite estimation was done on the base of previous research for countries of the Sahelian Zone. For the latter two, adequate ground data was available for correlation with satellite images.
 

1.2 BACKGROUND ON REMOTE SENSING

1.2.1 REMOTE SENSING

Remote sensing is the science and art of obtaining information about an object, area or phenomenon through the analysis of data acquired by a device that is not in contact with the object, area, or phenomenon under investigation (KIEFFER & LILLESAND,1987). As the term indicates, it applies to any information gathering device or method where the object of observation is remote from the device.

Out of a number of devices involved in remote sensing, the most common platforms are aircraft and satellites. The sensors associated with these devices are of two types, namely passive and active sensors. In a passive system, the instrument gathers information from the radiation that happens to arrive. The main sources of radiation for such systems are either solar radiation or thermal emissions. In the active system, it is the instrument itself on board the device that is the source of radiation. It sends signals to target under investigation, and receives the return signal, having the unique characteristics of the target features. As far as satellite remote sensing is concerned, systems operating in the visible and infrared part of the electromagnetic spectrum are passive while microwave instruments are either active or passive.

Currently, satellites are the main devices in remote sensing. And the two main types of satellites are the Polar or Near-polar Orbiting and Geostationary satellites. The Polar or Near Polar orbiting satellites are Sun-synchronous i.e. the satellites keep a precise pace with the Sun's westward progress as the earth rotates so that they always cross the equator at precisely the same solar time. Examples can be Landsat and NOAA satellites.

Geostationary satellites are satellites which travel with an angular velocity that matches the earth's rotation. As a result, they remain at the same point above the earth at all times. An example is Meteosat. These satellites are helpful in obtaining constant and persistent image of a particular area at fixed interval which is a great advantage in monitoring a location with high temporal resolution to capture the transient behavior of objects such as rain clouds.
 

1.2.2 HISTORICAL DEVELOPMENT OF REMOTE SENSING

Remote sensing at first started through the launch of small rockets in 1890's to just have a view on the earth's features at a height even though it began seriously during the period of 1940's using small cameras on board rockets. Though there was a remarkable progress, as remote sensing wasn't the main mission, it precluded the development of modern remote sensing techniques.

Through the development of meteorological satellites, imaging the earth was made possible. It began in 1960's by launching TIROS-1 satellite. Even though the images obtained was rather indistinct, it was made more distinct through the refinement of sensors on board in later years.

During the successive years, remote sensing advanced through the launching manned satellites such as Mercury, Gemini, and Apollo. In one of Apollo missions, the first controlled experiments involving the acquisition on multi-spectral photographs of earth features was made.

In 1975, Skylab, the first American space workshop, was launched with equipment such as 13-channel multi-spectral scanners. From 1981 onwards, space shuttles were used, which provided the widest spectral range of images of all the manned missions.

As manned missions are of short duration, the amount of useful survey information obtained is minimal. To satisfy the need for more comprehensive coverage, Landsat-1 (ERTS-1-Earth Resources Technology Satellite) was launched. This was the first unmanned satellite specifically designed to acquire data as an experiment to test the feasibility of collecting earth resource data from such satellites. As the data obtained was useful, other Landsats were launched (Landsat-1,2,3,4,5,6,& 7). Meanwhile, Spot satellites, which are near polar orbiters, were launched by France for commercial purposes.

Through time, more meteorological satellites were launched by numerous countries. These satellites were designed specifically to assist global weather prediction and monitoring.
 

1.3 SIGNIFICANCE OF ESTIMATION OF BIOMASS PRODUCTION USING
        REMOTE SENSING

In Eritrea approximately 80% of national energy consumption is in the form of biomass. Furthermore it is the primary energy supply of approximately 80% of the population. In Eritrea, the shortage of energy at the household level is so severe that it can be justly termed an energy crisis. The per capita consumption of energy is only 0.3 tones of oil equivalent (toe) compared to 0.71 toe for the rest of the developing world. For household energy consumption approximately 97% is biomass. Therefore, any developments in the energy sector which improve the conditions of the average Eritrean household must confront constraints of supply, demand, and production of biomass on both the national and regional levels.

Estimation of biomass production will provide guidance to energy development polices including:

- the impact of improved stoves on fuel wood and dung energy consumption.
- the potential of increasing the supply of fuel wood through the establishment of small scale "forest plantations"
- the potential of dung and other fuels for biomass energy supply.

The earth receives solar energy at the range of 5.4*10²⁴ Joule per year (A.E.DIXON & J.D.LESLIE,1979). This is equivalent to about 30,000 times total human consumption at the present time. To utilize this energy, the nature and amount of solar irradiance at a given location must be known. In other words, the distribution of intensity across the country must be known if solar devices such as solar powered electricity and water pumping are to be installed appropriately.

Rainfall distribution maps have a great importance in the study of desertification and drought prevention. Eritrea is pre-dominantly semi-arid, and is very sensitive to climatic fluctuations and moisture availability. Therefore, studying the rainfall distribution and vegetation response will help in taking measures against desertification, and will assist in quantifying the nation's water resources.

1.5 LITERATURE REVIEW

Satellite remote sensing of primary production for Sahel region was studied by S.D.Prince (Prince,1991) for years 1981-1988. Field measurements of primary production in semi-arid grassland for three Sahelian countries was analyzed in relation to multi-temporal sums of vegetation indices. The results showed that there is a linear relationship between vegetation index and seasonal primary production in the range of 0 - 3,000 kg/ha with the confidence interval ±(61 - 161)kg/ha.

A comparison and relationship between vegetation response and rainfall in the Sahel and East Africa was studied by Sharon E.Nicholson et.al. (S.E.NICHOLSON,1990) with the result that the spatial patterns of annual integrated NDVI closely reflect mean annual rainfall. Besides, there is a good relationship between monthly rainfall variations and NDVI especially for areas where the mean annual rainfall ranges from 200 - 1200 mm (the rainfall range of most areas of Eritrea). The correlations were good between NDVI and both the previous month's rainfall and were best between NDVI and the total of previous two month's rainfall.

A monthly mean of irradiance of Eritrea for July, August, September, October, and November months of the year 1994 was done by K.Blum et.al.(K.BLUM,1996) using the modified Heliosat method. In the Heliosat method, visible Meteosat images are used to calculate a Clear Sky Index (which is the fraction of radiation received relative to clear sky conditions). Their method first determines relative apparent albedos using a relation proposed by Diabate et al. Using these albedo values they calculated a satellite-derived cloud index which is determined from the ground albedo, the albedo of compact cloud cover, and the observed image albedo (which presumably has partial cloud cover).

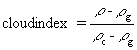
where

In a standard Heliosat method, cloud index is then linearly correlated with ground observations of global radiation to determine radiation distributions from satellite images. In a modified Heliosat method, a model is developed for contributions to image pixel counts from atmospheric scattering in the clear atmosphere. A semi-empirical equation relating the atmospheric scattering as a function of sun zenith angle, satellite zenith angle, and sun-satellite angle is used. Using the three parameter model to factor out atmospheric scattering contributions allows one to calculate a revised satellite-derived cloud index which can be related to the clear sky index using the simple relation:-

where K_clear = clearness index, and n = cloud index

In this study, we examine the applicability of conceptually simpler but more empirical image-radiation correlation techniques.

2. PRINCIPLES INVOLVED

2.1 SOURCES OF ELECTROMAGNETIC (EM)- RADIATION

EM radiation is the energy resulting from the acceleration of electric charges and the associated electric and magnetic fields (this study is restricted to radiation emitted from the Sun and earth's surface). EM radiation is governed by the equations

where the speed of light c²=1/(m e )

The energy associated with EM waves can be regarded as stream of photons travelling at speed of light, each photon having an energy hv, where h is Plank's constant and v is the frequency of the light. The EM spectrum, which is the range of wavelengths over which electromagnetic radiation extend, constitute of radio waves, micro waves, thermal infrared, infrared, visible, ultraviolet, x-ray, and gamma rays in decreasing order of wavelengths.

The ultimate source of energy for remote sensing is the Sun. Besides, all matter above absolute zero temperature emit radiation. Thus terrestrial objects are also sources of radiation, though it is considerably different in magnitude and spectral composition than that of the Sun. The emitted radiation from terrestrial objects is a function of temperature. From the principle of Black Body Radiation, the density of radiant energy U(v) emitted from a black body in the frequency range v+dv and v is:

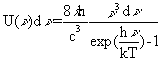
which is the Planck distribution law. The total energy density overall frequencies is

where a is a universal constant.

The intensity emitted from an object is therefore

This is the Stefan - Boltzman Law

The spectral distribution of emitted energy varies with temperature as shown in Figure 1. Meanwhile, the wavelength at which greatest energy density occur varies inversely with temperature and is given by Wein's displacement law:

2.2 ENERGY INTERACTION IN THE ATMOSPHERE

Atmosphere can have a profound effect on the intensity and spectral composition available to any sensing system as the radiation which reaches the sensed object passes through a certain optical path length of atmospheric air. These effects are caused principally through the mechanism of atmospheric scattering and absorption.

2.2.1 SCATTERING

As stated above, the atmosphere can have a significant effect on the incoming and outgoing radiation by scattering. There are three types of scattering depending on the size of particle involved. And these are Rayleigh scattering, Mie scattering and Non-selective scattering where Rayleigh and Non-selective scattering are the limiting cases of Mie scattering.

For Rayleigh scattering to occur, the particle size must not be larger than about 1/10^th of the wavelength of the light. In a gas with N molecules per unit volume and refractive index n, the Rayleigh extinction coefficient a for a wavelength is approximately

The extinction coefficient decreases as a wavelength increases. Specifically, the amount of scattering is inversely proportional to the fourth power of wavelength.

Mie scatter occurs for particles whose diameter is approximately equal to the wavelength. In a gas containing N spherical particles of radius R, the effective cross-section is given by

where Ads - is the volume in which the gas is contained, provided that no one particle lies in the shadow of another particle. If no absorption takes place, the extinction coefficient equals to scattering extinction co-efficient. Mie extinction coefficient is given by

where K = the extinction factor

The ratio of scattered to incident light can be expressed as

In this type of scattering, as the particles are of the order of wavelength, the light scattered from one part of the surface can be out of phase with coming from another part, unlike Rayleigh scattering were there is no phase difference between the light source and the scattered light. For Mie scattering, phase difference will be small for small scattering angle which gives rise to a large intensity in the forward direction and less in the reverse.

Non-selective scattering occurs when the diameter of the scattering particles is much larger than the wavelength. Water droplets, for example, cause such a scattering. They commonly have diameter in the range 5 to 100m m and scatter all visible wavelengths, equal quantities of blue, green, and red light are scattered, making fog and clouds appear white.

2.2.2. ABSORPTION

When light pass through a certain optical path in the atmosphere, it experiences absorption in addition to scattering by the existing particles. The intensity of the light diminishes according to

where a is the absorption coefficient

In the atmosphere, the most efficient absorbers of radiation are water vapor, carbon dioxide, and ozone.

The effect of this absorption is to leave only few regions known as atmospheric windows, in which the atmosphere transmits a substantial proportion of electromagnetic radiation. These are the only regions that can be used in remote sensing of the earth's surface.

Both scattering and absorption increase with increase in path length or with an increase in air mass.
 

2.3 ENERGY INTERACTION WITH THE EARTH'S SURFACE

When a light wave is incident on a surface, it will be reflected, transmitted, or absorbed. Furthermore, the energy of the absorbed radiation can be re-emitted as other forms of radiation. For an incident wave of intensity I_o the intensity of the reflected wave is rI_o and the amplitude of the rest is (1 - r)I_o, where r is the coefficient of reflection.

When EM radiation is incident on a given surface feature, out of the three fundamental processes the reflected part is often of interest in remote sensing. (thermal emission are also often of interest). The reflected part (rI_o) will be different for different earth features depending on the type of material and the condition of the material (e.g. dry or wet). Reflectivity is also dependent on the wavelength or frequency of the incoming radiation. The function which describes the dependence of reflectivity on wavelength is called the spectral reflectance function, and is given by

Different objects have very distinct spectral reflectance curves. It is the differences in spectral reflectance that allows one to distinguish different materials and objects using remotely sensed reflected radiation.

For thermal infrared wavelengths, the reflected radiation is outweighed by the emitted energy of the surface features. Hence in the thermal infrared, the radiation received from an object depends on its emissivity and temperature. Meanwhile, the temperature of an object will depend on its absorptivity (how much radiation it absorbs), its thermal conductivity (rate at which heat pass through a material), thermal capacity (ability of a material to store heat), and thermal inertia (thermal response of material to temperature change). Since our investigation focuses on non-thermal images, we will not discuss thermal remote sensing methods in detail.
 

2.4 DATA ACQUISITION AND INTERPRETATION

Detection of EM energy can be performed either photographically or electronically. The process of photography uses chemical reactions on the surface of a light sensitive film to detect energy variation within a scene while electronic sensors generate in electrical signals that corresponds to the energy or intensity of the detected radiation. The advantage of visual (photographic) is that it is simple, it provides high good spatial detail (because of the high resolution of chemical films) and geometric integrity (geometry is not distorted). On the other hand, electronics have the advantage of broader spectral sensitivity and easier conversion of the image to digital form.

Photographic images are interpreted visually (or scanned to convert them into digital images) whereas electronic images are interpreted digitally. The electronic image constitutes an array of pixels which vary in the level of brightness in accordance with the radiation received from the surface feature they represent. Pixel brightness is converted to a binary number. In our case pixel values are 8-bit binary numbers representing integer values from 0 to 255. These are positive integers that result from quantizing of the original electrical signal from the sensor.
 

2.5 REMOTE SENSING OF BIOMASS PRODUCTION

2.5.1 REFLECTANCE CHARACTERISTICS OF GREEN PLANTS

Green plants have a unique spectral reflectance curve as shown in the Figure 4. In the visible part of the spectrum, plants strongly absorb light in the blue (0.45m m) and red (0.67nm) regions and reflect strongly in the green portion of the spectrum due to the presence of chlorophyll. In cases where the plant is subjected to stress or to a condition which hinders growth, the chlorophyll production will decrease. And this in turn leads to less absorption in the blue and red bands.

In the near infrared portion of the spectrum (0.7 - 1.3m m), green plant reflectance increases to 40 - 50% of incident light. Beyond 1.3m m, there are dips in the reflectance curve due to absorption by water in the leaves.
 

2.5.2 PRINCIPLES OF DETECTION

The differential reflection of green plants in the visible and infrared portion of the spectrum makes possible the detection of green plants from satellites. Other features on the earth surface don't have such a unique step-like character in the 0.65 - 0.75m m range of the reflectance curve. NDVI is commonly used to represent this character. It is calculated from Advanced Very High Resolution Radiometer (AVHRR) data from NOAA-8 and NOAA-9 polar orbiting satellite and is defined as

where CHN1 and CHN2 are reflectance in the visible (red) (0.58 - 0.68m m) and near infrared channels (0.725 - 1.10m m) respectively. NDVI is determined by the degree of absorption by chlorophyll in the red wavelengths, which is proportional to green leaf density. Therefore, NDVI correlates well with green leaf biomass, leaf area index, and other related parameters (S.H.NICHOLSON,1990).

2.5.3 ESTIMATION OF RADIATION USE EFFICIENCY IN PLANTS

Plants make use of specific energy wavelengths (0.4 - 0.7m m) for the process of photosynthesis. The photosynthetically active radiation constitutes about 50% of the energy that is emitted from the sun. Out of this photosynthetically active radiation (PAR), about 80% of the radiation incident on a plant leaf is captured by photosynthetically active compounds. The rest is lost by reflection and absorption by non-photosynthesizing materials. A minimum of eight photons are required to produce a glucose from a single carbon-dioxide and glucose stores 28% of the captured energy in the form of chemical energy of the molecules (L.Burnham,1993). And finally, as the plant produces the glucose molecule it will use about 40% of the converted energy for dark respiration. Therefore, the maximum photosynthetic efficiency is

This result applies to c₄ plants (so-called because their first product of photosynthesis is 4-carbon sugar). For c₃ plants, like wheat and rice, the efficiency is lower due to photo-respiration effects (L.Burnham,1993).
 

2.6 REMOTE SENSING OF RADIATION INTENSITY

2.6.1 SOLAR CONSTANT

The average solar irradiance received outside the earth atmosphere is called Solar Constant. The intensity of Solar radiation above the earth's atmosphere has nearly constant value unlike irradiance received at the ground. It's average value is 1367 W/m² though it shows some variation due to variations in solar activity. Annual fluctuations due to Earth-Sun distance give rise to a variation of ±3.4% of the extra-terrestrial irradiance and is given by

where <E₀> is the mean value of solar constant, D is the Julian days
 

2.6.2 RADIATION REFLECTED AND RECEIVED BY THE GROUND

Radiation received at the ground surface is a combination of direct radiation, which comes from the sun after passing through a path length in the transparent atmosphere, and diffuse radiation which is radiation reflected by clouds and scattered by atmosphere in general. The contribution of diffuse radiation to irradiance received by ground depends on the atmospheric thickness, moisture content, cloud frequency, turbidity of the atmosphere, and angle of zenith.

The radiation that is reflected from the ground is very small compared to that reflected from the clouds. Its value depends on the reflectance of different earth surface features. In many cases, surface albedo is taken to be uniform (0.15) across the land.
 

2.6.3 ATMOSPHERIC EFFECTS

Atmosphere plays a major role at attenuation and reflection of light that pass through it. Its main effect are reflection, absorption, and scattering, depending on the wavelength and air mass ratio.
 

2.6.3.1 Air Mass Ratio

Air mass ratio is defined as the ratio of the path length of the radiation through the atmosphere at a given angle of a reference path length. The reference path length is that obtained by light traveling to a point at sea level straight through the atmosphere (vertically). The air mass ratio depends on the angle of zenith and the height above sea level of the observer. For small angles, the ratio is expressed as

where Q _z is the zenith angle. As the angle of zenith increases, the air mass ratio increases i.e., the attenuation increases.

2.6.3.2 Atmospheric Absorption and Reflection

Light passing through the atmosphere experiences absorption, scattering and reflection. Absorption causes heating and eventual re-emission of the absorbed energy as long wavelength radiation. Scattering is a wavelength dependent change in a direction. On the average 30% extra-terrestrial irradiance is reflected to outer space mainly due to cloud.
 

2.6.4 IRRADIANCE VARIATION

Irradiance received at a given location may differ in magnitude from hour to hour, day to day, month to month, and season to season depending on air mass, turbidity, moisture content, cloud frequency, and angle of zenith. The seasonal variation give rise to a significant amount of fluctuations in the irradiance received. This fluctuation in irradiance is due to variation in the declination angle from season to season. The declination angle (d ) that the earth posses with respect to the sun varies from season to season. In the middle of march and september the declination angle, d , is zero (0° ), where as d =23.5° and d =-23.5° in the middle of June and December respectively. Analytically, the declination angle is expressed as :-

where D is the Julian days.

Depending on the latitude, for a given declination angle, the irradiance increases or decreases. Moreover, irradiance varies with latitude. As shown in Figure 5, irradiance variation due to seasonal variation is great at high latitudes.

Variation in the earth sun distance also contributes to the variation in irradiance received although its contribution is very small.
 

3. METHODOLOGY

3.1 METHOD FOLLOWED FOR ESTIMATION OF BIOMASS PRODUCTION

3.1.1  Production of 10 day composite images

Images for the estimation of biomass production were obtained from a receiving ground station in Meteorology Department, Civil Aviation. The images are of NOAA satellite's Advanced Very High Resolution Radiometer (AVHRR) which has a spatial resolution of 1km by 1km. Images of the earth's portion are taken at five different channels. From these available channels, the most important channels for the study of biomass and leaf reflectance in general are Channel 1 (0.58 - 0.68m m), which is in the visible region, and Channel 2 (0.725 - 1.1m m) which is in the near infrared region though other channels such as Channel 5 are incorporated to screen out the clouds. Using the two channels Normalized Difference Vegetation Index (NDVI) is calculated for each day using the relation

The relation-ship between NDVI and Pixel brightness is :

where P is the pixel value

PIXEL	NDVI
83	0.0
109	0.1
135	0.2
161	0.3

Afterwards, ten days (decade) maximum NDVI value image i.e, three image for a month, is extracted. The reason for maximizing the NDVI value for a decade image is to minimize atmospheric effects, including cloud contamination.

3.1.2 Production of quality images

The images that are obtained from the Meteorological Department, Civil Aviation, are ten day maximum composite image which have passed through the above process. These images are for the months March, April, June and July for year 1996. The images for these four months were not clear enough to analyze and proceed through the study due to incorporation of noise during image capture by the satellite receiver. In addition to noise, other extraction and processing errors gave rise to

- shifted images: locations have an erroneous latitude and longitude
- noise in images: some pixels have unusually very high NDVI values
- screening of large areas by cloud mask

To minimize these effects and errors, Image Display and Analysis (IDA) software facility was used. Depending on the extent of the noise and contamination on the images, different methodologies were used to preprocess the images. These included filtering an image, replacing pixels of a decade image having erroneous values by pixels of the neighboring decade's image. The procedure followed for each images is explained in Table 1. Afterwards, the three decade images for each month were averaged so as to represent the average NDVI of the month.

3.1.3 Production of biomass maps

To utilize NDVI images to estimate biomass production, ground data should be collected to correlate or calibrate with the satellite observations. But such data does not yet exist for Eritrea. Therefore we utilize correlation studies performed in similar climate regions, including the West African Sahel. The most relevant study is one by S.D. Prince which reviews correlations between NDVI and biomass for a wide range of studies. He finds that the correlations relationship does not depend on either the year or the Sahelian country in which the study was performed. According to S.D.Prince, the equation that relates the two parameters i.e., Tree leaves plus above ground biomass (kg/ha) and NDVI, for three months of rainy season is:-

with r² value of 0.73 for 79 stations. The confidence interval associated with it is:-

NDVI days	confidence interval (kg/ha)
3	± 104
10	± 99
20	± 216
25	± 287

Using the above relation, the following equations were used for each month.

for months which have 30 days i.e, June and April, and

for months having 31 days i.e., July and March.

Onwards, using IDA facility, each picture element was made to represent the biomass production according to the above equation for each month. In order to do that each ranges of pixel brightness were assigned different colors (maximum of 16 colors) ranging from black to white i.e., modifying the look-up table, according to the equations. After inserting legends and names using IDA, the biomass scaled map was produced. The maps are illustrated in an appendix.

3.1.4 Estimation of biomass yield

In addition to producing biomass production maps, we calculated summary biomass production statistics. These statistics include monthly biomass production for both latitude-longitude grid cells, and production estimates for the old provinces (Hamassien, Senhit, Semhar, Barka, Gash-setit, Akeleguzai, Seraye, Sahel, Denkalia).

The IDA program has a statistics extraction utility which calculates average pixel values above a given threshold. The relevant threshold for biomass estimation is that NDVI value below which no production is expected. For each region of interest we estimate the biomass production by calculating the area of the productive pixels and the average NDVI for these pixels as follows:

where n = number of pixels in the region above threshold,
p = production of biomass production (kg/ha)
and 114.2 = area coverage of one pixel in hectares

A Fortran program was used to calculate production from the extracted pixel statistics. We report results for March, April, June, and July.

3.2 METHOD FOLLOWED FOR PRODUCTION OF RADIATION MAPS

For processing, analyzing, and producing radiation maps, Image Display and Analysis (IDA) and Lotus software were used. The month November, 1995 was chosen for the analysis. The method used for producing the radiation maps for November is described below.

3.2.1 Extraction of quality raw images

The Meteosat images available for November (see Table 2) are not complete. For some hours the image set is more than 50% complete. But for several, the majority of images are corrupted by noise or the positioning of the image is in error. The analysis was performed for those hours where the image set was more than 50% complete; these hours are 9am, 10am, 11am, and 3pm.

3.2.2 Processing of raw images

Images which were considered to be fit for the analysis were processed in the following manner. Appropriate minimum and average images for the series of raw images were done for 9am, 10am, 11am, and 3pm using IDA software processing facility. Afterwards, the difference image of the average and minimum was produced using the image algebra (A - B), where A and B represent the average and the minimum images respectively. While doing so, great care was taken to minimize errors due to the integer arithmetic used in the processing program.

3.2.3 Processing of ground data

Ground data is available for six stations: Asmara, Filfil, Shambuko, Sheeb, Omhajer,and Tzerona. The ground data contains relative humidity, temperature, rain, wind direction, and wind speed in addition to the radiation for each station. The data is sampled by an automated data logger in 15 minute intervals. The pyranometer measures the cumulative daily radiation since 00:00 hours. Cumulative radiation measurements are reported in units of calories per centimeter squared. In order to convert the reported cumulative radiation to 15 or 30 minute average radiation intensities, the following difference was taken:

where i = time in consideration

Csol(i) = radiometric cumulative measurement for time i

Dsol(i) = difference of cumulative radiometric measurement

Then the difference of cumulative radiometric measurement (Dsol) was changed to irradiance using the equation:-

where E(i) = irradiance in W/m², and where the time interval between i+1 and i-1 is 30 minutes. A Fortran program was used to perform these calculations. The appropriate correction factor to extract the direct irradiance from the total radiation received by the ground is :

where the angle of zenith is:

m = number of month

Eo = irradiance at altitude of the station involved

For November the angle of zenith was calculated to be about 35° . According to ROGER G.BARRY (BARRY, 1992), irradiance varies with altitude as

where E = irradiance at sea level (1000 W/m²)

Z = altitude of station in kilometers

The correction factor obtained following the above procedures shown in the following table:

 

Station	correction factor (CF)
Asmara	1.10
Sheeb	1.00
Shambuko	1.03
Filfil	1.00
Tzerona	1.01
Omhajer	1

 

To be more accurate, for the effect of variation in earth-sun distance, Eo must be modified again by (Cracknell, 1981):

where D stands for the julian days, E = 1000 W/m². For this study these effects were omitted as their effect was found to be minor.

3.2.4 Correlation of images with the ground data

The difference image produced for each hour was then correlated with the corresponding irradiance of the hour. As the correlation obtained was encouraging (see Table 3) further treatment was done. Using the IDA algebra, an image was produced for each hour, where the pixel value was normalized to be one fourth of the irradiance in units of W/m². The equation used for this calculation is :-

where DP = pixel of the difference image

E = irradiance

P = modified pixel

3.2.5 Extrapolation

For hours which have less than 50% images of the month, extrapolation method was used as the available raw images were inadequate to represent the respective hours. These hours are 12am, 1pm, and 2pm. The method used in extrapolating is as follows :-

 

where I₁₂, I₁₃, I₁₄ are extrapolated difference images for 12am, 1pm, and 2pm, and I₁₁ and I₁₅ are difference images for 12am and 3pm.

In order to test the linear extrapolation, correlation of the above difference images produced was done with the ground data. The result show that the r² value is greater than 0.63, which is a good agreement with the ground data.

3.2.6 Production of hourly radiation maps

After going through the above procedures, a range of pixel brightness was assigned a color by modifying the look up table with an interval of 50 or 100 W/m² for every hour of the processed image. Afterwards, the palette was then modified for convenience of printing. By inserting appropriate legend and names, images of each hour were produced.

3.2.7 Production of daily average radiation for November

By taking the average of the hours of the day, regression analysis was made between pixel reading of the average image and the radiometric cumulative measured output (csol) for each stations. And by using the regression equation, the image was made to read radiation in terms of KW-hr/m² by using IDA algebra. Furthermore, the look-up table was modified so as to set colors in steps of 0.25 or 0.5 KW-hr/m². Finally, by inserting legend and names to the image, the daily radiation map for November was produced.

3.3 METHODS FOLLOWED FOR PRODUCTION RAINFALL MAPS

The majority of the vegetation in the African Sahel region, including Eritrea, shows a rapid response to rainfall (S.E.NICHOLSON,1990). This rapid vegetation response to rainfall causes rainfall and green leaf cover to be correlated. This correlation assists in mapping rainfall amounts of different regions of interest. There is a clear physical basis for the relationship between NDVI and rainfall. NDVI is a measure or estimate of the amount of radiation being absorbed by plants. The amount of radiation absorbed is directly related to evapotranspiration, since the plant must cool primarily by evaporating water. The evapotranspiration is constrained by the amount of water in the soil. And for relatively low rainfall amounts, the amount of water in the soil is constrained by rainfall. Hence NDVI correlates with rainfall.

To produce the rainfall maps, historical rainfall records were used for stations which had a sufficient length of record. Normally, rainfall data of the same year is used for this type of correlations. But the unavailability of such data constrained us to utilize average historical rainfall values. Historical rainfall averages of over 20 years, compiled by Dr.Robert Van Buskirk (sources - Civil Aviation and Fantoli), of January, February, March months were correlated with NDVI of March and April of the year 1996 with different combinations. The reason for choosing these months is to estimate mainly the historical rainfall distribution of Bahri region. This is because, it is the only region that receives an appreciable amount of rain during this period. The stations involved are 25 in number. These are Mrara, Sabur, Damas, Nefasit, Adi Keyh, Adi Ugri (Mendefera), Dekemhare, Sen'afe, Zigfet, Abba Maitan, Fagena, Filfil, Gheleb, Ghinda'e, Nakfa, Akurdet, Barentu, Kullucu, Keren, Asmera, Belesa, and Mitsiwa'e (Massawa). The procedure followed for estimating rainfall distributions are as follows.

3.3.1 Extraction of NDVI values

From March and April images, Normalized Difference Vegetation Index (NDVI) was extracted for each pixel for the above stations. This was done using Image Display and Analysis (IDA) software extraction facility.

3.3.2 Regression analysis

Afterwards, historical rainfall was correlated with the extracted NDVI value of the stations using Lotus software. Regression analysis of the NDVI was made for each month with different combinations of the rainfall. To mention some of the different trials, NDVI of the stations was correlated with

- concurrent month of historical rainfall

- concurrent plus previous month of historical rainfall

- concurrent plus two previous month of historical rainfall

- previous month

- previous two months

There were times when correlation coefficients obtained were not satisfactory. For those cases, other possibilities were tried such as

- excluding some stations with suspected erroneous values

- producing two correlation relations: Bahri and rest of Eritrea

- producing correlations for each decade of the month

- adding more stations in regions of interest

3.3.3 Production of rainfall distributions

The rainfall distributions were produced by utilizing that relation which has the highest r² value out of the several correlations that were examined. Rainfall maps were produced for January, February, and March. The historical rainfalls were represented on an image by modifying the look-up table according to the regression equations. Finally, after inserting legends and names using IDA, rainfall distribution maps were produced.

4. RESULTS

4.1 RESULTS ON BIOMASS PRODUCTION

Monthly production of biomass for March, April, June, and July is illustrated in the Appendix. March biomass production (tree leaves plus above ground biomass) is mostly concentrated across the Bahri region with an amount that ranges from 750 - 1000 kg/ha. Across south and south-western part of Eritrea, the production is rather small, which ranges from 0 to 250 kg/ha. There is no visible production of biomass tree leaves and herbs for Barka and Denkalia provinces. The reason for such a localized biomass production across Bahri region for this time of the year is due to the peculiar rain distribution. Moisture in the lower layers of the atmosphere coming from the Gulf of Aden and the Red Sea falls on a limited portion of the Eastern Escarpment as cool marine air flows through the passes in the Adi Teklezan-Ghizghiza-Keren area. This gives rise to rain along the eastern escarpment of the highland due to orographic effects. At the far north of Eritrea and near the Sudanese border, there is a small scale biomass production ranging from 250 - 500 kg/ha. This rainfall area is produced from the same moisture source and precipitates from orographic effects as the marine air moves inland near Aqiq. April biomass production across the country in general is less than that of March due to a decrease in rainfall in March and April months. And this is visible especially for Bahri region, where there is a considerable decrease in biomass output. In Barka and Denkalia regions, there is no significant biomass detected during both March and April except for a small amount along the Barka river.

For June, the winds blow across the south-west of Africa carrying moisture and giving rainfall in the south and south-west parts of the country. For Gash-setit, Seraye and Akeleguzai regions the production ranges from 250 - 750 kg/ha where as across Bahri it is less, 250 - 500 kg/ha. For the sake of comparison, in Gonder, Ethiopia the production ranges from 500 - 1500 kg/ha for the same time of the year. For July, the production amount and coverage increases due to increasing rainfall amounts and expanded distribution. As a result, for some places on southern part of Eritrea the production reaches 1500 kg/ha. Biomass production across the highlands of Eritrea is generally in the ranges of 250 - 500 kg/ha. For Denkalia and some portions of Barka, there are no indications of production.

Table 4 shows the estimated biomass production per province (the old provinces). Peak biomass production for March and April occurs in Hamassein with 0.142 and 0.068 million metric tones respectively. Denkalia has the smallest production of all the provinces. For June and July, Gash-Setit has the highest total amount of production per region with 0.394 and 0.490 million metric tones respectively. Production in terms of 0.5° cells is shown in Table 5, where the cells represent specific areas labelled in Figure 10. Cell 42 contains highest aggregate biomass for March, cell 17 for April, while cell 15 for June and July. Table 6 shows the total biomass production (tree leaves plus above ground biomass) for Eritrea for the months of March, April, June, and July which are 0.58, 0.26, 0.77, and 1 million metric tones respectively. The corresponding confidence intervals are ±0.164, ±0.06, ±0.109, and ±0.131 million metric tones respectively.

4.2 RESULTS ON RADIATION MAPPING

The regression analysis made for each hour between satellite derived pixel and ground data is shown in the Appendix. Radiation received by satellite, which is expressed as pixel brightness, is inversely related to irradiance measured at the ground stations. The reason is clouds tend to reflect brightly than earth surface features. Therefore, bright pixel corresponds to reflectance from the cloud while low brightness pixel corresponds to reflectance albedo of the ground. The correlation coefficient obtained for each hour ranges from 0.8 to 0.93 as shown on Table 3.

Coming to the radiation maps of each hour, generally, the intensity increases from 9 am to 12 am and decreases afterwards. The 9 am radiation shows that most regions of Eritrea have intensity ranging 480 - 520 W/m² except for those which are along the eastern escarpment which is in the range of 400 - 440 W/m². The associated RMS error is about ±17 W/m².

For 10 am, the intensity across the country increases proportionally as the incidence angle of the radiation increases i.e., angle of zenith decreases. On the Western and South-western parts of Eritrea, the intensity ranges 600 - 720 W/m² while in some places of the Barka the intensity is less. In Denkalia region, the intensity ranges 660 - 680 W/m² though the value decreases on the eastern escarpment due to clouds. The associated RMS value is about ±18 W/m².

For 11 am, even though the intensity increases globally, across the eastern escarpment it is relatively low (approx. 640 W/m²) for the hour due to clouds. Generally, intensity for the country for 11 am is in the range of 700 - 740 W/m² while for noon it is 800 - 840 W/m². For noon the intensity on the Red Sea just off the coast of Denkalia reaches 840 - 880 W/m². The associated RMS error is about ±19 W/m².

From noon onwards, the intensity starts to decrease. For 1 pm, in the South and Southwest, the intensity is about 760 - 800 W/m². On the eastern escarpment, there is an intensity ranging from 600 to 660 W/m², which is very thin in width and long in length. On the upper portion of the Red Sea, the intensity is 720 - 760 W/m² while on the lower it ranges from 760 to 800 W/m². The RMS error for this hour is about ±28 W/m².

Onwards, for 2 pm and 3 pm, the intensity decreases uniformly. Across the South and Southwest, the intensity decreases from 680 to 720 W/m² for 2 pm, and to about 540 - 570 W/m² for 3 pm. On the eastern escarpment, the intensity is very low (160 - 280 W/m²) for 3 pm. And on the upper portion of the Red Sea, the intensity is rather low compared to the intensity on the lower portion due to clouds. RMS error for 2pm and 3pm is about ±33 W/m² and ±24 W/m².

Regression analysis made between average intensity of the day and the cumulative irradiance obtained from the ground stations show that the r²-value is 0.93. The output of the regression analysis is :-

where Pixel = average pixel value for the day

Rad = radiation in KW-hr/m²

We illustrate the Radiation map produced utilizing this regression equation. The map shows average daily solar energy received per meter squared of November. Across the South and West of Eritrea, the energy received is about 5.5 - 5.7 kW-hr/m² while on the eastern escarpment it is 3.5 - 4.3 kW-hr/m². In Akeleguzai and the upper portion of the Red Sea it ranges from 5.1 kw-hr/m² to 5.5 kw-hr/m² and on some parts of the upper portion of the Red Sea, just off the coast, it reaches 4.7 - 5.1 W/m². The associated RMS error is about ±0.133 kW/m².(see Table 7)

4.3 RESULTS ON RAINFALL CORRELATIONS

Out of the many possibilities on the regression analysis for January, February, and March historical rainfalls, the best r² value was obtained for March NDVI vs January Rain, March NDVI vs February Rain, and April NDVI vs March Rain. These r² values range from 0.81 to 0.86. This result shows that NDVI of a month don't correlate with rainfall of the concurrent month but with rainfall of the previous month as there is a time lag in plants utilizing the available soil moisture which is attributed to rainfall. Therefore, for these months, NDVI correlates with the previous two months of rainfall. The regression outputs are shown Table 8.

For January, February, March months, the historical rainfall distribution is restricted to the eastern escarpment especially to Bahri region. For January, few parts of the Bahri region have rainfall greater than 140 mm, such as Filfil. Other stations such as Faghena and Abba Maitan have rainfall in the ranges of 100 - 140 mm. On February there is increase in spatial coverage of rainfall across Bahri region. Significant locations have rainfall in the range of 60 - 140 mm. On March, the rainfall width decreases suddenly to an extent that most locations on Bahri have rainfall 0 - 40 mm. The spatial width of the distribution decreases significantly. The RMS error for January, February, and March is ±17 mm, ±30 mm, and ±17 mm respectively.(see Table 9)

5 CONCLUSION

NDVI correlates well linearly with biomass production. As Eritrea is situated in the Sahel region, it has the same climatic distribution as the rest of countries in that zone. Therefore, having correlation relation between NDVI and tree leaves and above ground biomass production for Sahelian countries will help estimating biomass production of this country. The confidence interval of the total production for each month is about 13% to 28% of the production for the month. Therefore, the result gives a rough estimate of production of Eritrea. A more accurate method of estimating requires an extensive field work to come up with a regression relation between NDVI and ground data in .

For production of radiation maps, difference image of average and minimum images of the month November correlates well with ground measured irradiance for the hours under consideration. The regression analysis between the ground irradiance data and difference image will enable the production of radiation maps with an average RMS error of about 5% of the average irradiance of each hour. The assumption that ground albedo is uniform across Eritrea will give rise an additional error. The reason for not taking this effect under consideration through the study is because IDA fraction and division processing ability is not accurate. However, in order to estimate this error, test was done for 9 am by adding an another term for correcting the above assumption. In the region of interest, the variation obtained in the pixels due to the correction factor is about 3 pixels which is 15 W/m² of intensity. This will give rise to an additional error of about 2% in the production. Correction factor of the ground, correction factor of atmospheric scattering, and correction factor due to geometry of sun- earth-satellite relative position will give rise to an additional error.

Historical rainfall correlates well generally with NDVI of the next month for the year 1996. In fact, better correlation can be obtained if the NDVI is correlated with the same year rainfall data. The unavailability of recent data of rainfall hindered the production of a more accurate rainfall distribution. However, average of rainfall of over 20 years can also help in producing rainfall distribution as a particular year rainfall data is similar to some extent though there is fluctuations in the amount of rainfall from year to year. For the production of rainfall distribution maps, the RMS error produced for Bahri region ranges from 15 - 25% of the average rainfall of that region for months January, February, and March.

APPENDIX

TABLE 1: PROCEDURES FOLLOWED FOR RAW NDVI IMAGES

IMAGES	COMMENT	PROCESS
Nva29.img  (march1d)	clouds exist in the Red Sea, Eth. Highlands and Sahel	Cloud mask area replaced with first decade values
N7A12.img  (march1d)	clouds exist in Akeleguzai	Cloud mask area replaced with first decade values
N7e16.img  (march1d)	clouds exist in Eth. and Denkalia	Cloud mask area replaced with first decade values
NGA15.img (march2d)	clouds on Eth. highlands	cloud mask area replaced with second decade values
NFA20.img (march2d)	clouds on the Red Sea	cloud mask area replaced with second decade values
NIB28.img (march2d)	noise exists in image, cloud across highlands of Eth., Sahel, and Red Sea	filtered with minimum, filtered with maximum,  cloud mask are replaced with second decade values
NGB1B.img (april2d)	cloud in Denkalia and Eth. highlands	cloud mask area replaced with second decade values
NHB1O.img (april2d)	clouds on Eth. highlands	cloud mask area replaced with second decade values
NDVD1696.img(june1d)	noise in the image clouds in Eth.	filtered with minimum, filtered with maximum,  cloud mask area replaced with filtered images of the same month
NDVD1796.img(june2d)	noise in the image  cloud over Akeleguzai	filtered with minimum, noise generated extreme values were replaced with first decade values,  filtered with maximum, cloud mask area replaced with filtered images of the same month
NDVD1896.img(june3d)	noise in image  little cloud over Eritrea	filtered with minimum, noise generated extreme values were replaced with first decade values,  filtered with maximum, cloud mask area replaced with filtered images of the same month
NDVD1996.img(JULY1D)	noise in image  little cloud in Eth.	filtered with minimum, noise generated extreme values were replaced with second decade values,  filtered with maximum, cloud mask area replaced with filtered images of the same month
NDVD2096.img(july2d)	cloud across Akeleguzai	cloud mask area replaced with filtered images of the same month
NDVD2196.img(july3d)	noise in image  spots of cloud exist	filtered with minimum, noise generated extreme values were replaced with second decade values,  filtered with maximum, cloud mask area replaced with filtered images if the same month

 

TABLE 2: AVAILABLE VISIBLE IMAGES FOR NOVEMBER

Date	9am	10am	11am	12am	1pm	2pm	3pm	4pm	5pm	av%
1	M	M	M	M	M	M	M	M	M	0
2	M	M	M	M	M	M	M	M	M	0
3	M	M	M	M	M	M	M	M	M	0
4	M	M	M	M	M	M	M	M	M	0
5	M	M	M	M	M	M	M	M	M	0
6	M	M	M	M	M	M	M	M	M	0
7	M	M	M	M	M	M	M	M	M	0
8	M	M	M	M	M	M	M	M	M	0
9	M	M	M	M	M	M	M	M	M	0
10	M	M	M	M	M	M	M	M	M	0
11	M	M	M	M	M	M	M	M	M	0
12	M	M	M	M	M	M	M	M	M	0
13	M	M	M	M	M	M	M	M	M	0
14	OK	OK	M	M	M	M	OK	M	M	33
15	OK	OK	OK	M	OK	M	OK	M	M	56
16	OK	OK	OK	M	M	M	OK	M	M	44
17	OK	OK	OK	M	M	M	OK	M	M	44
18	OK	OK	OK	OK	OK	OK	OK	OK	OK	100
19	OK	OK	OK	OK	OK	OK	OK	OK	OK	100
20	OK	OK	OK	M	M	M	OK	M	M	44
21	OK	OK	OK	M	M	M	ERR	M	M	33
22	OK	OK	OK	M	M	M	OK	M	M	44
23	OK	OK	OK	M	M	M	OK	M	M	44
24	OK	OK	OK	M	ERR	ERR	OK	ERR	ERR	44
25	OK	OK	OK	OK	OK	OK	OK	OK	OK	100
26	OK	OK	OK	OK	OK	OK	M	M	M	67
27	OK	OK	OK	M	M	M	OK	M	M	44
28	OK	OK	OK	M	M	M	OK	M	M	44
29	OK	OK	OK	M	M	M	OK	M	M	44
30	OK	OK	OK	M	M	M	OK	M	M	44

LEGEND OK= IMAGE IS AVAILABLE

M = IMAGE IS MISSING

ERR=IMAGE IS CORRUPTED

TABLE 3: HOURLY IRRADIANCE REGRESSION OUTPUTS

Hour	r² - value	co-efficient	constant
9am	0.640223	-5.47842	515.1971
10am	0.762099	-6.09255	690.7722
11am	0.772107	-5.02632	800.7319
12am	0.803200	-7.76977	854.0025
1pm	0.629796	-5.88545	798.0598
2pm	0.880843	-8.31333	707.3686
3pm	0.852340	-10.6775	577.7570

where the equation relating the above parameters is

DP - pixel of the difference image

TABLE 4: BIOMASS PRODUCTION FOR MARCH, APRIL,

JUNE, JULY,1996 IN MILLION METRIC TONES

PROVINCES	MARCH	APRIL	JUNE	JULY
HAMASSIEN	0.1420	0.0680	0.0620	0.0830
SENHIT	0.0560	0.0220	0.0500	0.0740
SEMHAR	0.0320	0.0055	0.0010	0.0001
AKELE-GUZAI	0.1100	0.0430	0.0660	0.0470
SAHEL	0.0340	0.0250	0.0230	0.0380
SERAYE	0.0750	0.0460	0.1600	0.2420
BARKA	0.0140	0.0030	0.0110	0.0110
GASH-SETIT	0.1000	0.0050	0.3940	0.4900
DENKALIA	0.0170	0.0005	0.0007	INSIGNIFICANT
TOTAL	0.580	0.260	0.770	0.990

TABLE 5: BIOMASS PRODUCTION PER 0.5° CELL IN TONES

0.5° cells	MARCH	APRIL	JUNE	JULY
1	5486	1003	INSIG	INSIG
2	INSIG	INSIG	INSIG	INSIG
3	186	INSIG	INSIG	INSIG
4	10447	49	650	INSIG
5	4530	200	INSIG	INSIG
6	INSIG	INSIG	INSIG	INSIG
7	INSIG	INSIG	INSIG	INSIG
8	2632	INSIG	INSIG	INSIG
9	10384	304	INSIG	INSIG
10	INSIG	INSIG	INSIG	INSIG
11	INSIG	INSIG	INSIG	INSIG
12	INSIG	INSIG	INSIG	INSIG
13	14759	5746	7893	13638
14	7330	3376	120000	160000
15	12914	12970	260000	300000
16	33246	17215	140000	170000
17	60234	50854	140000	160000
18	36250	30415	90185	120000
19	39199	38607	50382	95289
20	20559	10814	56295	32648
21	INSIG	INSIG	INSIG	INSIG
22	INSIG	INSIG	INSIG	INSIG
23	INSIG	INSIG	INSIG	INSIG
24	INSIG	INSIG	INSIG	INSIG
25	4382	1388	929	2080
26	13261	3279	38757	34367
27	29201	17562	130000	160000
28	33246	16041	97598	130000
29	33259	18094	95329	150000
30	25338	16067	46455	91412
31	24465	21321	28912	39325
32	17797	8478	15268	2824
33	8	INSIG	INSIG	INSIG
34	8	INSIG	INSIG	INSIG
35	INSIG	INSIG	INSIG	INSIG
36	18430	6397	3432	5920
37	13496	4136	1808	1418
38	13010	3258	18118	23540
39	14660	4199	22470	27074
40	21537	7332	36642	33533
41	49723	23710	43035	58400
42	120000	40323	37633	18989
43	41645	4262	656	4
44	INSIG	INSIG	INSIG	INSIG
45	23234	14565	2706	3897
46	1334	48	72	115
47	3407	373	1120	176
48	6721	2217	3259	1802
49	24544	7951	24322	45220
50	71617	39917	33747	52796
51	8723	5213	788	294
52	307	22	INSIG	INSIG
53	16368	16639	995	6233
54	217	7	INSIG	INSIG
55	28	471	12	INSIG
56	1995	975	5741	5226
57	12223	4858	15977	23444
58	3900	501	228	742
59	INSIG	INSIG	INSIG	INSIG
60	INSIG	INSIG	INSIG	INSIG
61	2	181	16	INSIG
62	500	406	20	7
63	12381	9242	14623	17818
64	1546	1328	80	205
65	134	1288	INSIG	INSIG
66	INSIG	INSIG	INSIG	INSIG
67	1588	835	1741	964
68	6010	2072	1575	4669
69	475	16	INSIG	INSIG
70	20714	3577	959	4147
71	INSIG	INSIG	INSIG	INSIG

where INSIG - insignificant

TABLE 6: BIOMASS PRODUCTION OF ERITREA WITH THE ASSOCIATED

CONFIDENCE INTERVAL

MONTH	BIOMASS PRODUCTION OF ERITREA IN MILLION METRIC TONES
MARCH	0.58 ± 0.16
APRIL	0.26 ± 0.06
JUNE	0.77 ± 0.11
JULY	0.99 ± 0.13

 

TABLE 7: RMS ERROR FOR EACH HOURS OF THE DAY

AND FOR DAILY AVERAGE SOLAR RADIATION

HOURS	RMS ERROR
9 AM	± 17 W/m²
10 AM	± 18 W/m²
11 AM	± 19 W/m²
12 AM	± 28 W/m²
1 PM	± 33 W/m²
2 PM	± 24 W/m²
3 PM	± 35 W/m²
DAILY AVERAGE SOLAR RADIATION	± 0.133 KW-hr/m²

 

TABLE 8: HISTORICAL RAINFALL vs NDVI REGRESSION OUTPUTS

Relations	r² value	coefficient	constant
March NDVI vs January R.	0.899153	381.7109	-8.489792
March NDVI vs February R	0.859322	399.3003	-6.791150
April NDVI vs March R.	0.814744	229.1804	5.109377

where the equation relating these parameters is

TABLE 9

RMS ERROR FOR HISTORICAL RAINFALL DISTRIBUTION

FOR JANUARY, FEBRUARY, AND MARCH

MONTH	RMS ERROR
JANUARY	± 17 mm
FEBRUARY	± 30 mm
MARCH	± 17 mm

BIBLIOGRAPHY

HANS G.BEYER, CLAUDO CONSTANZO, AND DETLEV HEINEMANN, MODIFICATION OF THE HELIOSAT PROCEDURES FOR IRRADIANCE ESTIMATES FROM SATELLITE IMAGES, SOLAR ENERGY, 1996, VOL.56, NO.3, 207-212, ELSEVIER SCIENCE Ltd

KONRAD BLUM, ANNETTE HAMMER, DETLEV HEINEMANN, AND MESFIN YOHANNES, SATELLITE DERIVED IRRADIANCE MAPS FOR ERITREA, 1996, DEPARTMENT OF PHYSICS, CARL VON OSSIETZKY UNIVERSITY

LAURIE BURNHAM, THOMAS B.JOHANSSON, HENRY KELLY, AMULA K.N.REDDY, ROBERT H.WILLIAMS, RENEWABLE ENERGY : SOURCES FOR FUELS AND ELECTRICITY, 1993 ISLAND PRESS

ARTHUR CRACKNELL AND LANDSON HAYES, INTRODUCTION TO REMOTE SENSING, 1991, COPYRIGHT A.P.CRACKNELL AND L.W.B.HAYES

ARTHUR P.CRACKNELL, REMOTE SENSING IN METEOROLOGY, OCEANOGRAPHY, AND HYDROLOGY, 1981, ELLIS HORWOOD LIMITED

M.L.DAVENPORT AND S.E.NICHOLSON, ON THE RELATION BETWEEN RAINFALL AND THE NORMALIZED DIFFERENCE VEGETATION INDEX FOR DIVERSE VEGETATION TYPES IN EAST AFRICA, INT.J.REMOTE SENSING, 1993, VOL.14, NO.12, 2369-2389, TAYLOR & FRANCIS Ltd

A.E.DIXON AND J.D.LESLIE, SOLAR ENERGY CONVERSION, 1979, UNVERSITY OF WATERLOO

S.M.E.GROTEN, NDVI - CROP MONITORING AND EARLY YIELD ASSESSMENT OF BURKINA FASO, INT.J.REMOTE SENSING, 1993, VOL.14, NO.8, 1495-1515, TAYLOR & FRANCIS Ltd

THOMAS M.LILLESAND AND RALPH W.KIEFER, REMOTE SENSING OF IMAGE INTERPRETATION , 2^ND EDITION, 1987,JOHN WILEY AND SONS, Inc.

J.W.TWIDELL & A.D.WEIR

KUO-NAN LION, INTRODUCTION TO ATMOSPHERIC RADIATION, INTERNATIONAL GEO-PHYSICS SERIES, VOL.26, 1980, ACADEMIC PRESS Inc.

JURGEN R.MEYER, INTRODUCTION TO CLASSICAL AND MODERN OPTICS,

1972, COPYRIGHT JURGEN R.MEYER

SHARON E.NICHOLSON, MICHAEL L.DAVENPORT, AND ADA R.MALO, A COMPARISON OF THE VEGETATION RESPONSE TO RAINFALL IN THE SAHEL AND EAST AFRICA, USING NORMALIZED DIFFERENCE VEGETATION INDEX FROM NOAA AVHRR, CLIMATIC CHANGE 17, 1990, 209-241, KLUWER ACADEMIC PUBLISHERS

N.A.QUARMBY, M.MILNES, T.L.HINDLE, AND N.SILLEOS, THE USE OF MULTI-TEMPORAL NDVI MEASUREMENT FROM AVHRR DATA FOR CROP YEILD ESTIMATION PREDICTION, INT.J.REMOTE SENSING, 1993, VOL.14, NO.2, 199-210, TAYLOR & FRANCIS Ltd

F.L.SNIJDERS, RAINFALL MONITORING BASED ON METEOSAT DATA - A COMPARISON OF TECHNIQUES APPLIED TO THE WESTERN SAHEL, INT.J.REMOTE SENSING, 1991, VOL.12, NO.6, 1331-1347, TAYLOR & FRANCIS Ltd

GRANT W.PETTY, THE STATUS OF SATELLITE - BASED RAINFALL ESTIMATION OVER LAND, REMOTE SENSING ENVIRON.51, 1995, 125- 137, ELSEVEIR SCIENCE Inc.

M.B.POTDAR, SORGHUM YIELD MODELLING BASED ON CROP GROWTH PARAMETERS DETERMINED FROM VISIBLE AND NEAR-IR CHANNEL NOAA AVHRR DATA, INT.J.REMOTE SENSING, 1993, VOL.14, NO.5,895- 905, TAYLOR & FRANCIS Ltd

S.D.PRINCE, SATELLITE REMOTE SENSING OF PRIMARY PRODUCTION: COMPARISON OF RESULTS FOR SAHELIAN GRASSLANDS 1981-1988, INT.J.REMOTE SENSING, 1991, VOL.12, NO.6,1301-1311, TAYLOR & FRANCIS Ltd.

C.J.TUCKER, W.W.NEWCOMB, S.O.LOS, S.D.PRINCE, MEAN AND INTER-YEAR VARIATION OF THE GROWING-SEASON NORMALIZED DIFFERENCE VEGETATION INDEX FOR THE SAHEL 1981-1989, INT.J.REMOTE SENSING, 1991, VOL.12, NO.6, 1133-1135, TAYLOR & FRANCIS Ltd

JOHN TWIDELL AND TONY WEIR, RENEWABLE ENERGY RESOURCES, 1986,

J.W.TWIDELL & TONY WEIR

B.K.WYLIE, J.A.HARRINGTON, S.D.PRINCE, SATTELITE AND GROUND-BASED PASTURE PRODUCTION ASSESSMENT IN NIGER:1986-1988, INT.J.REMOTE SENSING, 1991, VOL.12,NO.6,1281-1300,TAYLOR & FRANCIS Ltd AKRAM A.ZUHAIRY AND A.A.M.SAYIGH, SIMULATION OF SOLAR RADIATION IN SAUDI ARABIA, RENEWABLE ENERGY, 1995, VOL.6, NO.2, 107-118, ELSEVIER SCIENCE Ltd