Chapter 4 Data Analysis and Results
Chapter 4
Data Analysis and Results
Data availability and reliability
Eritrea has not yet established a national meteorological centre that is responsible, among other things, for standardizing meteorological instruments and stations as well as methods of observations within the country according to the established and recommended international standards. Thus, lack of one central responsible body results in decentralized meteorological stations and observations by various governmental organizations mainly Ministry of Agriculture, Meteorological Services of the Civil Aviation Department and Water Resource Department.
This decentralized approach resulted in:
Unlike those of the Ministry of Agriculture and the Meteorological Services, most of the stations under the Water Resource Departments are automatic and their readings are not collected on real-time basis. In this study the gauge data from the Ministry of Agriculture and Meteorological Services are used. The Cold Cloud Duration (CCD) data used is obtained from the Department of Meteorology of the University of Reading Data Archives and these include CCD with threshold temperatures of –30, -40, -50 and –60oC. Ten-day cumulative CCD and rainfall from 1994 to 1997 are the data used in this study.
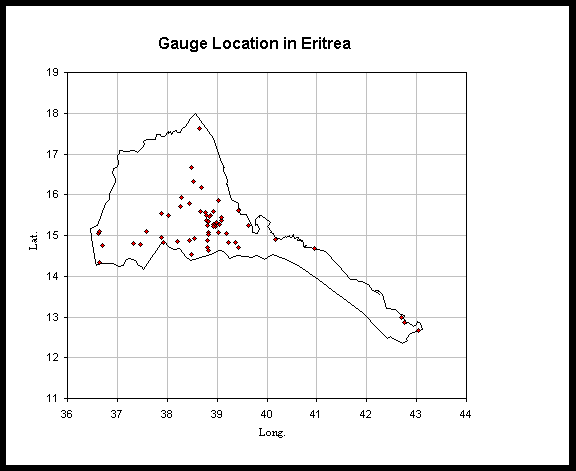
Most of the rainfall stations in the country are located over densely populated areas particularly over the highlands and southwestern lowlands of the country (Fig. 4.1). The non-uniform distribution of gauge over the country might be ascribed to the population distribution and agricultural and hydrological significance. The existing station network over the coastal areas, eastern escarpment and the northwestern lowlands are insufficient for this study. Moreover, the non-uniform and non-standard instruments, orientations, exposure and methods of observations within the country might make the accuracy and reliability of the data questionable. Thus, bearing in mind the accuracy and reliability of gauge data; the results should be used cautiously.
Fig. 4.1 Station network (stations used in this study)

The analysis is done using TAMSAT Rainfall estimation technique and its purposes are:
Cold Cloud Duration (CCD) at thresholds -30, -40, -50 and –60oC are extracted from satellite image pixels for all available gauge rainfall stations in the country. In Excel all gauge data are imported and combined with the corresponding CCD values.
Determination of Best Threshold TemperatureComparing CCD values at different thresholds with rain gauge data of the zone does the determination of best threshold temperature for each zone. As discussed in the preceding chapter, the optimum temperature threshold determination for each calibration zone is easily done using the following contingency table.
|
CCD = 0 |
CCD > 0 |
||
|
Gauge = 0 |
n 11 |
n 12 |
|
|
Gauge > 0 |
n 21 |
n 22 |
Where n11 is the number of occasions having both gauge records and CCD values are zero,
n
12 is the number of occasions having gauge records zero but CCD values non-zero,n
21 is the number of occasions having gauge records rainfall but CCD values is zero,n
22 is the number of occasions having gauge records and CCD values are non-zero,In n11 and n22 both gauge and satellite values agree each other but they disagree in n12 and n21. Thus the optimum temperature threshold is the one in which:
Previous TAMSAT calibrations were done using the contingency table. However, in this analysis, instead of contingency table, accuracy and bias are calculated for each grid square and the optimum thresholds (high accuracy and low bias) for each grid square are then determined from the accuracy and bias analysis (Fig. 4.5 and Appendix 3). This new approach is used because the number of gauges (data points) used in this study is not sufficient to determine optimum threshold using contingency table approach.
In this study determination of best threshold is done in Excel. The data is organised in columns of country name, station, longitude, latitude, dekad, gauge value and CCD of different thresholds in separate columns (Table 4.1). This is done for each month from June to September. In order to see the station distribution gauge location is plotted as shown in Fig. 4.1. The region is gridded into one-by-one degree grid square (Fig. 4.2) and each grid cell is numbered starting from the topleft. Then for each station a grid cell number is assigned and the cell number for each station is included in separate column of the worksheet. Moreover, grid cell midpoint-longitude and -latitude are calculated and included in other columns of the worksheet.
Mid-Longitude=36+1/2+1*INT((Long.-36)/1) [4.1a]
Mid-Latitude=19-1/2-1*INT((19-Lat.)/1) [4.1b]
Where 36 and 19 are the top-left longitude and latitude and 1 is the width of the grid square.
Table 4.1 Worksheet format
|
Ctry |
Stn |
Long |
Lat. |
Date Code |
Rain |
CCD30 |
CCD40 |
CCD50 |
CCD60 |
Grid No |
Mid grid long. |
Mid grid lat. |
|
ER |
MHM |
38.65 |
17.62 |
97061 |
0.0 |
20 |
16 |
12 |
7 |
11 |
38.5 |
17.5 |
|
ER |
MHM |
38.65 |
17.62 |
97062 |
0.0 |
10 |
7 |
5 |
1 |
11 |
38.5 |
17.5 |
|
ER |
MHM |
38.65 |
17.62 |
96062 |
0.0 |
8 |
3 |
2 |
0 |
11 |
38.5 |
17.5 |
|
ER |
MHM |
38.65 |
17.62 |
94061 |
0.0 |
2 |
1 |
0 |
0 |
11 |
38.5 |
17.5 |
|
ER |
MHM |
38.65 |
17.62 |
95061 |
0.0 |
2 |
1 |
0 |
0 |
11 |
38.5 |
17.5 |
|
ER |
MHM |
38.65 |
17.62 |
96061 |
0.0 |
2 |
1 |
0 |
0 |
11 |
38.5 |
17.5 |
|
ER |
MHM |
38.65 |
17.62 |
97063 |
13.0 |
1 |
1 |
0 |
0 |
11 |
38.5 |
17.5 |
Date Code means yymmdk (i.e. year, month and dekad)
Fig. 4.2 Grid Square Map
The analysis is done for each CCD threshold and any row with either missing rain gauge or CCD is deleted from the sheet. The data were sorted by station and then the sub-total rainfall and CCD of a particular month for the years 1994 to 1997 is calculated for each station. Each sheet contains data on Grid number, Longitude, Latitude, Date, Rainfall, CCD threshold, Grid cell number, Mid-longitude and –latitude of grid cell.
In order to identify the best CCD threshold temperature that discriminates rain from no-rain each CCD threshold temperature is classified into success, too warm and too cold. Successes (n11 + n22) are defined when there is no gauge rain and zero CCD (i.e. Rain=0 and CCD=0 for a particular gauge) or when there is rain and CCD (Rain>0 and CCD>0 for a particular gauge). Too Warm (n12) means when there is CCD but no gauge rain (i.e. Rain = 0 and CCD > 0). Too Cold (n21) means when there is rain but no CCD (i.e. Rain > 0 but CCD=0). Successes, too warm and too cold are calculated for all data points and each is given a value of either 1 or 0. For example, if the data point is success 1 is assigned in the success column and 0 is assigned in the too warm and too cold columns for that particular data point. Having done the above, the whole data is sorted by success and too warm in descending order and thereby classified into three classes (success, too warm and too cold) for plotting. Then a map that shows a distribution of successes, too warm and too cold is plotted for all months and different CCD thresholds (Fig. 4.3). Note that the gauge in figure 4.3 are outside Eritrea for the month of June. This is because for June northern Ethiopia gauges are also used.
Fig. 4.3 Distribution of success, too warm and too cold by station for selected CCD threshold
Fig. 4.3 Distribution of success, too warm and too cold by station for selected CCD threshold (cont…)
Fig. 4.3 Distribution of success, too warm and too cold by station for selected CCD threshold (cont…)
The preceding figures show the distribution of successes, too warm and too cold by station. Identifying best CCD threshold with high accuracy (n11+ n22>> n12+ n21) and equal distribution of too warm and too cold (no bias in either end i.e. n12@ n21) was the aim of this analysis. However, from the above-congested figures it became difficult to identify such optimum threshold and thus the following further analysis was carriedout.
The distribution of successes, too warm and too cold is processed and plotted for each grid square rather than for each station. The data were sorted by grid number and then sub-total rainfall and CCD threshold temperature of a particular month for the years 1994 to 1997 was calculated for each grid number rather than station names. The sheet contains columns on grid number, successes, too warm, too cold, total sums of successes, too warm and too cold, accuracy, bias, mid-longitude and mid-latitude. Too warm (n12) and too cold (n21) were calculated for each grid number. The successes were divided into two: n11 and n22. Success of no rain and zero CCD (i.e. Rain=0 and CCD=0) is denoted by n11 and success of rain and none-zero CCD (Rain>0 and CCD>0) by n22. Accuracy and bias are then calculated as follows:
Sum = (n11+ n12+ n21+ n22) [4.2a]
Accuracy = (n11+ n22) / Sum [4.2b]
Bias = (n21- n12) / Sum [4.2c]
A high accuracy and low bias is considered to be a best CCD threshold that discriminates rain from no-rain. The accuracy is then classified into five different classes i.e. below 20%, 20-50%, 50-70%, 70-90%, and above 90% and on the other hand the bias is classified into three categories: cold bias (< -20%), no bias (-20% to +20%), and warm bias (>20%). The result obtained from this analysis is shown in the following figures. Therefore, from the accuracy and bias maps and graphs indicated in the following figures (fig. 4.4 and 4.5) optimum threshold is determined for each grid square.
Fig 4.4 Accuracy and Bias for different CCD thresholds for each month
Fig 4.4 Accuracy and Bias for different CCD thresholds for each month (Cont…)
Fig. 4.5 Graph of Accuracy and Bias for grid square
Fig. 4.5 Graph of Accuracy and Bias for grid square (Cont…)
Constant Threshold Region (CTR) is a region within which rainfall is assumed to be similar or homogeneous and thus the best temperature threshold and the calibration parameters (i.e. ao and a1) are the same.
The accuracy and bias maps and graphs plotted in the preceding figures (figures 4.4 and 4.5) became useful and easy in identifying the best threshold for each grid square and thereby in delineating the Constant Threshold Regions (CTR). For each grid square in figure 4.5 and appendix 3 an optimum threshold (high accuracy and low bias) is selected. Each grid square with the same optimum threshold is then identified and thus amalgamated to form a calibration zone or Constant Threshold Region (Figure 4.6). Eritrea falls into two constant threshold regions. The highlands, southwestern lowlands and parts of the eastern escarpment lie under a homogeneous constant threshold region while the northern tip of the country and the eastern lowlands (coastal areas) lie under different constant threshold region (Fig. 4.6). Due to unavailability of gauge over the northwestern lowlands calibration was not carriedout.
Fig. 4.6 Constant Threshold Region (CTR)
Fig. 4.6 Constant Threshold Region
Regression of median gauge against mid-class CCD approach, that is useful for drought monitoring purposes, is used in the calibration. Days are classified according to CCD value and regression of median gauge in each class against mid-class CCD is used for the calibration. Only non-zero CCD values are used in calculating the calibration parameters ao and a1.
Determination of calibration coefficient and validation are done only for the Constant Threshold Region (CTR) that comprises the highlands, southwestern lowlands and parts of the eastern escarpment. For the other CTR that comprises the eastern lowlands and northern tip of the country the determination of calibration coefficient and validation are not done for the following reasons:
The calibration coefficients for the highlands, southwestern lowlands and parts of the eastern escarpment are done in the following ways. For each month stations that belong to the same Constant Threshold Region (CTR) are sorted and separated from the others. About thirteen CCD class intervals are defined and the CCD class number 1 to 13 is assigned to each class. Mid class CCD is calculated and for each CCD data their corresponding CCD class is derived. Median rain and number of data are also calculated for each CCD class (Table 4.7). CCD = 0 is excluded from this data set because of the assumption that when CCD = 0 rainfall is assumed to be zero. Regression analysis between mid class CCD and median rain is done as follows:
Table 4.2 Sample of worksheet used for determination of calibration coefficient
|
Station |
Long. |
Lat. |
Date Code |
Dekad |
Rain |
CCD30 |
CCD Class |
Mid Class CCD |
Class Limit |
Class No |
Median Rain |
No. of Data |
Estimated Rain |
|
AFABET |
38.68 |
16.18 |
95072 |
5 |
81 |
17 |
4 |
0 |
0 |
0 |
20.3 |
1 |
0 |
|
AFABET |
38.68 |
16.18 |
97071 |
10 |
67.4 |
21 |
5 |
3 |
1 |
1 |
4.5 |
45 |
20.13 |
|
AFABET |
38.68 |
16.18 |
94073 |
3 |
61.5 |
19 |
4 |
8 |
6 |
2 |
11.7 |
32 |
25.04 |
|
AFABET |
38.68 |
16.18 |
95073 |
6 |
53.5 |
36 |
8 |
13 |
11 |
3 |
19.75 |
50 |
29.94 |
|
AFABET |
38.68 |
16.18 |
97072 |
11 |
45.2 |
15 |
3 |
18 |
16 |
4 |
49.75 |
84 |
34.85 |
|
AFABET |
38.68 |
16.18 |
96071 |
7 |
25.5 |
11 |
3 |
23 |
21 |
5 |
51.9 |
56 |
39.75 |
|
AFABET |
38.68 |
16.18 |
96072 |
8 |
17 |
4 |
1 |
28 |
26 |
6 |
49.9 |
59 |
44.66 |
|
AFABET |
38.68 |
16.18 |
95071 |
4 |
6.7 |
13 |
3 |
33 |
31 |
7 |
49 |
47 |
49.56 |
|
AFABET |
38.68 |
16.18 |
97073 |
12 |
2.1 |
8 |
2 |
38 |
36 |
8 |
51 |
47 |
54.47 |
|
AFABET |
38.68 |
16.18 |
94071 |
1 |
0 |
1 |
1 |
45.5 |
41 |
9 |
66.9 |
26 |
61.82 |
|
AFABET |
38.68 |
16.18 |
94072 |
2 |
0 |
10 |
2 |
55.5 |
51 |
10 |
59 |
16 |
71.63 |
|
AFABET |
38.68 |
16.18 |
96073 |
9 |
0 |
1 |
1 |
65.5 |
61 |
11 |
13 |
5 |
81.44 |
|
GIZGZA |
38.52 |
16.33 |
97071 |
10 |
82.2 |
23 |
5 |
75.5 |
71 |
12 |
0 |
91.25 |
|
|
GIZGzA |
38.52 |
16.33 |
95071 |
4 |
43.9 |
15 |
3 |
81 |
13 |
0 |
17.19 |
||
|
GIZGZA |
38.52 |
16.33 |
97072 |
11 |
38.5 |
17 |
4 |
Slope |
0.98 |
||||
|
GIZGZA |
38.52 |
16.33 |
95072 |
5 |
37.5 |
27 |
6 |
Intercept |
17.2 |
||||
|
GIZGZA |
38.52 |
16.33 |
94073 |
3 |
27.7 |
21 |
5 |
Slope (a1) = (<xy><x><y>) / (<x2> - <x>2) [4.3a]
Intercept (ao) = <y> - a1<x> [4.3b]
Where x and y are mid class CCD and median rain, respectively and the sign < > indicates weighted means. The number of points in each class weights the mean. Thus, for the highlands, southwestern lowlands and parts of the eastern escarpment the slope (a1) and the intercept (ao) are shown in Table 4.8.
Table 4.3 Slopes and intercepts for highlands, southwestern lowlands and parts of the eastern escarpment
|
June (CCD40) |
July (CCD30) |
August (CCD30) |
September (CCD50) |
|
|
Slope (a1) |
0.75 |
0.98 |
0.55 |
0.88 |
|
Intercept (ao) |
4.38 |
17.19 |
20.72 |
1.71 |
Therefore, the calibration equations for the southwestern lowlands, highlands and parts of the eastern escarpment are:
Estimated Rainfall for June = 0.75CCD + 4.38 [4.4a]
Estimated Rainfall for July = 0.98CCD + 17.19 [4.4b]
Estimated Rainfall for August = 0.55CCD + 20.72 [4.4c]
Estimated Rainfall for September = 0.88CCD + 1.71 [4.4d]
Estimated Rainfall = 0 when CCD = 0 (for all months) [4.4e]
A scatter plot of mid class CCD against median rainfall is presented in Fig. 4.7. The observed linear relation and the R2 shown in the regression analysis are reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment.
Fig 4.7 Median rain against mid class CCD (June to September)
Fig 4.7 Median rain against mid class CCD (June to September)
In order to identify areas where the calibration algorithms and thresholds are inappropriate or needs further refinements and also to assess the skill of the estimate it is useful to evaluate the calibration.
Finally, using the calibration equations (Equation 4.4) for the constant threshold region that comprises the highlands, southwestern lowlands and parts of the eastern escarpment estimated rain is calculated. Plots of the estimated rainfall against gauge value are shown in Fig. 4.8. The validation is not done using an independent data set, however; it is done with the same data that are used in the determination of calibration coefficient (1994 – 97data).
The estimated rain is more or less reasonably good over most parts of the calibration zone. The evaluation indicated that there is a reasonable agreement between the satellite estimate and gauge value in all considered months (June to September). In June, July, August, and September over 76%, 67%, 60% and 83% of the stations respectively the gap between the satellite estimate and gauge value is less than 10mm – and this is reasonably good. Generally, the disagreement (gap) between the satellite estimate and gauge values occurs mainly due to under-estimate. The under-estimate does not occur in a particular climatic region, so it is difficult to identify a particular region where the calibration is under estimating.
Fig 4.8 Comparison between satellite estimate and gauge rainfall (July and August)
Fig 4.8 Comparison between satellite estimate and gauge rainfall (June and September)
Chapter 5 Discussions and Conclusions
Chapter 5
Discussion and Conclusions
Discussion
The calibration analysis is done for summer rainy season (June to September) which is the major rainy season for the highlands, southwestern lowlands and parts of the eastern escarpment. During normal years clouds usually develop over the eastern escarpment or its adjoining highlands and moves towards the western parts of the country. In line with that, the rain belt also move from the eastern parts of the country towards the west. During wet spells, low level moist southwesterly winds originated from Southern Hemisphere maritime high-pressure cells converge with the dry northerly winds along the InterTtropical Convergence Zone (ITCZ) (Fig. 2.8). Generally in a normal summer rainy season the highlands, parts of the eastern escarpment and southwestern lowlands receive more or less similar type of rainfall.
During the summer season, except occasional rain the northern tip of the country and the eastern lowlands (i.e. coastal areas) usually remain dry. Over the eastern lowlands wind generally descends towards lower altitude leaving it a rain shadow region. However, at times when big storm develops over the Yemen high ground it moves towards west and provides rain over the northern tip of the country and eastern lowlands. Thus, the rainfall over these climatic regions occurs when the rain-giving meteorological mechanisms are favourable in producing big storms over Yemen. Otherwise, frequent small storms over Yemen highlands give rain over Yemen and disappear without moving to the west and producing rain over eastern lowlands and northern tip of the country.
Based on the calibration analysis Eritrea falls into two Constant Threshold Regions (CTR): the first comprises the highlands, southwestern lowlands and parts of the eastern escarpment and the other comprises the eastern lowlands (coastal areas) and northern tip of the country. The calibration was not carried for the Northwestern Lowlands due to lack of gauge data. The separation into two constant threshold regions (CTR) can be explained in terms of the two different weather systems:
For the northern tip of the country and eastern lowlands –60oC is found to be the optimum threshold in all months June to September. Over the highlands, southwestern lowland and parts of the eastern escarpment –40oC in June, -50oC in September and –30oC in July and August are found to be the optimum threshold temperature. The linear relation between CCD and estimated rainfall is reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment. During the on-set (June) and cessation (September) of the summer rain the threshold for these regions is cooler than the thresholds within the season (i.e. July and August). This change in the threshold within the season can be explained in terms of weather producing systems as follows:
Table 5.1
R2 for highlands, southwestern lowlands and parts of the eastern escarpment. (The graph is shown in figure 4.7)|
June –40oC |
July -30oC |
August –30oC |
September –50oC |
|
|
R2 |
42% |
74% |
48% |
52% |
|
Intercept |
~ 6.5mm |
~ 12.5mm |
~ 21mm |
~ 5mm |
The northern tip of the country and the eastern lowlands (coastal areas) lie under -60oC Constant Threshold Region in all months June to September. This threshold is cooler than the threshold of the other constant threshold region (i.e. CTR that comprises the highlands, southwestern lowlands and parts of the eastern escarpment). The same and cooler threshold (-60oC) over these climatic regions (i.e. northern tip of the country and the eastern lowlands) is also in agreement to the fact that both receive rainfall from deep storm that migrated to these regions from Yemen highlands. That means they get rainfall from deep cloud and from the same weather system (migrated storms). It should also be noted that there is lack of adequate rain gauge data over the eastern lowlands (i.e. coastal areas) and the northern tip of the country. For the CTR that comprises the eastern lowlands and northern tip of the country the determination of calibration coefficient and validation are not done for the following reasons:
Stability of the calibration may be tested by using the calibration derived from one year in subsequent years as well as by showing how far a given algorithm is applicable beyond the limits of the area containing the stations used for calibration (Milford, J.R. and Dugdale, G., 1990). However, in this analysis it was difficult to do such type of evaluation for the reason that there were only four years (1994-97) data available for this study and these data are totally used for the calibration. No independent data is left to do the validation.
The evaluation, though done not with an independent data set, indicated that there is a reasonable agreement between the satellite estimate and gauge value in all considered months (June to September). In June, July, August, and September over 76%, 67%, 60% and 83% of the stations respectively the gap between the satellite estimate and gauge value is less than 10mm – and this is reasonably good. Thus, the calibration algorithm works well. However, in some cases, the satellite estimate is lower than the gauge value and this may be explained climatologically as follows.
No particular climatic region is particularly influenced by the under-estimate, under-estimate occurred in different stations from different climatic regions. Therefore, it is difficult to identify a particular climatic region where the calibration algorithm is underestimating.
The validation, however, should be carriedout by the kriging method using independent data from the current and / or next summer season. The Kriging method is useful in the validation because it estimates errors related to the density of gauge network. Using the kriging method satellite estimate is plotted against gauge data with error bars. Therefore, whenever the satellite estimate lies within the error bar the estimate is reasonably good, otherwise not good.
In Eritrea rainfall is mainly convective and thus it is highly localized and has great temporal and spatial variability. Moreover, the sparse raingauge network is not uniformly distributed throughout the country. Therefore, in order to measure area rainfall on real time basis as accurately as possible there is a need to supplement gauge data using satellite estimates. The Eritrean Meteorological Service installed PDUS (Primary Data Users System) and has an access to half-hourly and hourly Meteosat images. However, so far no quantitative estimate of rainfall is introduced. The result of this study, therefore, will be important in introducing satellite based rainfall estimate and augmenting the raingauge data to obtain real-time area rainfall estimate.
The aim of this study is to discuss briefly various satellite-based rainfall estimation techniques that are relevant to Eritrea type of climate and to calibrate the TAMSAT technique for Eritrean summer rainfall particularly over summer-rain receiving parts of the country. Of many available satellite-based rainfall estimation techniques microwave, CPC, ORSTOM and TAMSAT are briefly discussed. These techniques are chosen because they are relevant to Eritrea type of climate. The microwave technique uses microwave sensors for estimating rainfall but it is not fully developed for real-time daily operational application. The ORSTOM technique uses ground surface temperature obtained from meteosat images and it is based on the inverse relationship of previous rainfall on ground surface temperature (Guillot, 1995). This technique is tested in west Africa and when combined with cold top cloud frequency technique the ORSTOM technique resulted in greater accuracy. However, the technique needs surface data and is calibrated against contemporaneous gauge data and this may make the technique difficult to implement in Eritrea at this stage. The CPC technique uses meteosat satellite data, real-time raingauge data, model analysis of wind and relative humidity and orographic features (Herman et al, 1997) to estimate rainfall both from cold and warm cloud. This technique is calibrated against contemporaneous data but is the only technique to estimate rainfall from warm cloud. The CPC technique may be important for Eritrea in estimating winter rainfall (that is mainly from warm cloud). It is also useful for estimating occasional warm cloud summer rainfall.
The TAMSAT technique is the one that is calibrated for summer rainfall of Eritrea in this study. It uses half-hourly or hourly infrared images and depends on the assumption that convective clouds are the main source of rain. There is a direct linear relation between cold cloud duration and estimated rainfall. This technique is the only technique that is entirely pre-calibrated against historical gauge data. Moreover, it is automated and easy for operational application.
Hourly Cold Cloud Duration (CCD) at different thresholds and gauge data from 1994 to 1997 are used in this study. Analysis was carried out in order to: determine the optimum threshold that discriminates rain from no-rain, delineate constant threshold regions, calculate calibration coefficient, and estimate rainfall using the regression equation. The result of the analysis indicated that during summer Eritrea falls into two Constant Threshold Regions (CTR): the first comprises the highlands, southwestern lowlands and parts of the eastern escarpment and the second comprises the northern tip of the country and eastern lowlands (coastal areas). Due to lack of gauge data no calibration was done for the northwestern lowlands. As discussed in section 5.1.2., the separation into two constant threshold regions (CTR) can be explained in terms of the following two different weather systems: the northern tip of the country and the eastern lowlands receive occasional rainfall from deep cloud with cooler threshold; while the highlands, southwestern lowlands and parts of the eastern escarpment obtain similar type of rainfall from relatively warmer clouds.
For the northern tip of the country and eastern lowlands –60oC is found to be the optimum threshold in all months June to September. Over the highlands, southwestern lowland and parts of the eastern escarpment –40oC in June, -50oC in September and –30oC in July and August are found to be the optimum threshold temperature. The linear relation between CCD and estimated rainfall is reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment. For the CTR that comprises the eastern lowlands and northern tip of the country the determination of calibration coefficient and validation are not done because during summer large number of events over these regions is no-rain and this resulted in zero median gauge rainfall.
Over the highlands, southwestern lowlands and parts of the eastern escarpment changes in threshold within the season are observed and this is explained in terms of the strength and variability of rain-giving meteorological mechanisms. When the mechanisms are strong and favourable they provide rain from relatively warmer threshold (e.g. July and August), otherwise deep ascent and hence deep cloud with cooler threshold is required (e.g. June and September).
The evaluation, though not done with an independent data set, indicated that there is a reasonable agreement between the satellite estimate and gauge value in all considered months (June to September). In June, July, August, and September over 76%, 67%, 60% and 83% of the stations respectively the gap between the satellite estimate and gauge value is less than 10mm – and this is reasonably good. However, sometimes the satellite estimate is lower than the gauge value and this underestimate in all months might be explained in terms of the strength of the rain-giving meteorological mechanisms and availability of moisture. When there is enough moisture and favourable low level winds then relatively slight ascent with warmer threshold than the optimum gives rain. In this case the calibration algorithm underestimates.
No particular climatic region is particularly influenced by the under-estimate, therefore, it is difficult to identify a particular climatic region where the calibration algorithm is underestimating.
Future Direction
Satellite based rainfall estimation gives a real-time broader overview of rainfall that is useful for agriculture, famine warning, hydrology, pest monitoring and erosion. More specifically, this information is useful to know whether the rain is sufficient for crop growth or not; and to predict river flow, erosion and potential locust outbreak areas. For Eritrea, which is located in semi-arid region near the Red Sea, these information is extremely useful.
Therefore, the results obtained from this study are useful for operational application in Eritrea. While being operational, however, continuous validation must be carriedout by the kiriging method using independent data from the current and / or next summer season.
Further improvement to the satellite based rainfall estimation is essential and highly recommended in order to increase the accuracy of the estimate. To that end, in collaboration with TAMSAT group and other relevant organisations it is essential to improve the estimate by:
References
Barret, E.C. and D.W. Martin, (1981): The Use of Satellite Data in Rainfall Monitoring. Academic Press, london.
Barret, E.C and M.J. Beaumont, (1994): Satellite rainfall monitoring: an overview, in Remote Sensing Reviews, Goel, N.S and E.C. Barrett (eds.), pp 303-373. Harwood Academic Publications, USA.
Bonifacio, R. and Grimes, D.I.F, (1998): Rainfall Estimation Manual, Natural Resource Institutes
diplo, M., (1998): The influence of weather system on satellite rainfall estimation with application to river flow modeling.
ELIZABETH M. SHAW, 1994: Hydrology in Practice
Fantoli, Amilcare, (1966): Contributo alla Climatologia Dell’Altiplano Etiopico, Regione Eritrea.
Global Atmospheric Research Program (GARP) (1978): The West African Monsoon Experiment (WAMEX), GARP Publication Series No. 21.
Grimes, D.I.F., Milford, J.R and Dugdale G., (1993): The use of satellite rainfall estimates in hydrological modelling. Presented at the first international conference of the African Met. Soc. Nairobi, Kenya.
Guillot, B. (1995): Satellite et precipitations: Contraintes techniques et physiques, analyse de quelques methodes, problemes de recherche et de validation. Veille Climatique Satellitaire: 55, 27-58.
Habtemichael, A. and D.E. Pedgley, 1964: Spring Rainfall over Eritrea, Arch. Met. Geoph. Biokl, ser. A.23, 285-296
Herman, A., V.B. Kumar, P.A. Arkin and J.V. Kousky, (1997): Objectively determined 10-day African rainfall estimates created for famine early warning systems. Int. J. Rem. Sens.: 18, 2147-2159.
Houghton J.T and Taylor F.W., (1973): Remote sounding from artificial satellites and space probes of the atmospheres of the earth and the planets.
Kidder, S.Q. AND T.H. Vonder haar, (1995): Satellite Meteorology, an introduction. London: Academic Press.
Meteorological Map of Ethiopia, (1979), National Meteorological Services Agency, Ethiopia
Milford, J.R. and Dugdale G., (1990): Estimation of rainfall using geostationary satellite data, in Applications of remote Sensing in Agriculture, Steven, M.D. and J.A. Clark (eds.), pp 97-110. Butterworth, London.
Morland, J., D. Grimes, G. Dugdale and T. Hewison, (1997): The effect of the land surface on microwave rainfall estimates, in Proceedings of the 23rd Annual Conference and Exhibition of the Remote Sensing Society, Reading, pp 493-498.
Pedgley, D.E. (1966): The Red Sea Convergence Zone: Weather 21, 350-358 and 394-406
Ramage, C.S. (1971): Monsoon Meteorology, Academic Press
Spencer, R.W., H.M. Goodman and R.E. Hood, (1989): Precipitation retrieval over land and ocean with SSMI: Identification and characteristics of the scattering signal. J.Atmos. And Oceanic Tech.: 6, 254-273.
Stanley Q. Kidder and Thomas H. Vonder Haar, (1995): An Introduction to Satellite Meteorology.
Tesfaye Haile, (1982): Mean general atmospheric circulation over Ethiopia and its vicinity, Internal Report. National Meteorological Services Agency, Addis Ababa, Ethiopia.
Twomey, S., H. Jacobowitz and H.B. Howell, (1967): Light Scattering by cloud layers. J.Atmos. Sc.: 24, 70-79
Van Buskirk R. and Araia A., (1994): Rainfall Statistics of Eritrea. Environmental Information Collection and Analysis Project - Dept. of Physics, University of Asmara.