First and foremost praise be to the living, almighty and ever-loving God for all what He has done, He is doing and will continue to do in my life. Not forgetting His presence, protections and solutions whenever I call to Him in my distress.

I would like to express my profound heart-felt gratitude and appreciation to my supervisor and course co-ordinator Dr. D.I.F. Grimes for his invaluable guidance, advice, reviews and comments during the writing of this dissertation as well as for his kindness, patient, wonderful assistance and encouragement throughout the year. I will ever remain grateful to him.

I would also wish to express my deep appreciation to Mr. Hadgu Kibreab for his inestimable assistance in the writing of the dissertation. I am also grateful to all people whom I lived with in Reading who in one way or the other contribute to my studies and made my stay in Reading an enjoyable one.

Many thanks go to all my friends for their invaluable friendship and encouragement in my academic and professional progress. I am also grateful to my colleagues in the Eritrea Meteorological Service and Civil Aviation Department for their encouragement in my academic and professional progress.

Last but not least, I wish to express my unbounded sincere thanks to the Eritrea Civil Aviation Department for granting me the MSc study and to the World Meteorological Organisation and United Kingdom Government for awarding me voluntary co-operation programme (VCP) fellowship that enable me to undergo this study. My acknowledgement should also go to the Registrar of the UK Meteorological Office College, Mr. Ken C. Smith, for his hospitality and efforts in making the year a comfortable one.

1 Introduction *

2 Climate of Eritrea *

3 Satellite and Satellite Based Rainfall Estimation Techniques *

4 Data Analysis and Results *

5 Discussion and Conclusions *

APPENDIX 1 *

APPENDIX 2 *

APPENDIX 3 *

References *

The aim of this study is to discuss briefly various satellite-based rainfall estimation techniques relevant to Eritrea type of climate and to calibrate TAMSAT technique for Eritrea summer rainfall particularly over summer-rain receiving parts of the country. Microwave, CPC, ORSTOM and TAMSAT satellite-based rainfall estimation techniques are briefly discussed. The TAMSAT technique uses infrared images and depends on the assumption that convective clouds are the main source of rain.

Cold Cloud Duration at different thresholds and gauge data from 1994 to 1997 are used in this study. Eritrea falls into two Constant Threshold Regions: the first comprises the highlands, southwestern lowlands and parts of the eastern escarpment and the second comprises the northern tip of the country and eastern lowlands. The separation into two constant threshold regions can be explained in terms of the two different weather systems that occur over these two calibration zones. For the northern tip of the country and eastern lowlands –60^oC is found to be the optimum threshold throughout June to September. Over the highlands, southwestern lowland and parts of the eastern escarpment –40^oC in June, -50^oC in September and –30^oC in July and August are the optimum thresholds. The calibration is done for and found to be reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment.

Changes in threshold within the season are observed and this is explained in terms of the strength and variability of rain-giving meteorological mechanisms. When the mechanisms are strong and favourable they provide rain from warmer threshold (e.g. July and August), otherwise deep cloud with cooler threshold is required (e.g. June and September).

The evaluation, though not done with an independent data set, indicated that there is a reasonable agreement between the satellite estimate and gauge value. However, sometimes the satellite estimate is lower than the gauge value and this might be attributed to the fact that sometimes there might be enough moisture and favorable low level winds to give rain from warmer cloud than the optimum threshold. No particular climatic region is particularly influenced by the under-estimate. The validation, however, should be carriedout by kriging method using independent data from the current and / or next summer season.

1. Introduction

Eritrea is located in the East of Africa. It is within tropics and has a greatly varying topography. Its climatic region is generally classified into Western Lowlands, Highlands, Eastern Escarpment and Eastern Lowlands. Based on rainfall distribution, these major climatic regions further classified into eleven sub-climatic zones (Van Buskirk and Araia, 1994). The temporal variation of the climate over each climatic zone is mainly caused by large-scale changes in the monsoon flow. The Inter Tropical Convergence Zone (ITCZ), tropical cyclones over north Indian Ocean, orographic lifting, thermodynamic instability, mid-latitude low pressure systems and Red Sea Convergence are the main causes of rainfall over Eritrea. Eritrea has four distinct seasons. Autumn is mainly dry and cold over most parts of the country. In winter fog, dew and fall in minimum temperature are very common, however over the eastern escarpment and coastal areas it is rainy season. Spring is a short-rainy season for the highlands of Eritrea. Summer is a major rainy season for the highlands, western lowlands and parts of the eastern escarpment. The coastal areas also receive occasional rainfall during summer season due to migration of strong storm from Yemen highgrounds.

1. Climate of Eritrea

 

1. Eritrea and its Climatic Regions

Eritrea is located in the East of Africa. Djibouti and Ethiopia border it in the south, Sudan in the West and North and the Red Sea in the East. Its topography varies greatly within a short distance. There is a narrow strip of highlands in the central surrounded by lowlands on the west and escarpment and coastal area in the east.

Fig. 2.1 Map of Eritrea

 

 

 

 

 

 

 

 

 

The climate of Eritrea is generally sub-divided into the following climatic zones: the central highlands, western lowlands and eastern escarpment and lowlands (Van Buskirk and Araia, 1994). This classification is attributed to the rapid spatial variation of topography along the west-east direction. The central highlands are characterised by long rainfall season during summer, short rainy season during spring, and mild temperature throughout the year. High temperature and intense summer rainfall is the prevailing climate over the western lowlands while winter rainfall, large amount of cloud cover, high humidity and hot temperatures are the characteristics climate observed over the eastern escarpment and lowlands (coastal regions). The temporal variation of the climate over each climatic zone is mainly caused by large-scale changes in the monsoon flow. During Southern Hemisphere summer the prevailing wind over Eritrea is northeasterly and this is replaced by south westerly during the Northern Hemisphere summer. This reversal of wind is a behaviour of monsoon system (Ramage, 1971). Inter Tropical Convergence Zone (ITCZ), Tropical cyclone over north Indian Ocean, Orographic lifting, Thermodynamic instability, mid-latitude low pressure systems and Red Sea Convergence (Pedgley 1966) are the main causes of rainfall over Eritrea.

Fig. 2.2 Rainfall map of Eritrea: Isohyet analysis of mean annual rainfall (source: Fantoli, 1966)

 

 

 

 

 

 

 

 

 

 

 

 

2. Climatic Sub-regions

The climatic region of Eritrea is classified into Western Lowlands, Highlands, Eastern Escarpment and Eastern Lowlands. Based on rainfall distribution, it further classified into eleven sub-climatic zones (Van Buskirk and Araia, 1994).

Fig. 2.3 Sub-Climatic Zones of Eritrea (Source: Van Buskirk and Araia, 1994).

 

 

 

 

 

 

 

 

 

 

 

 

 

The Western Lowlands are sub-classified into three sub-climatic zones namely North Western Lowlands (NWL), South Western Lowlands and Hills (SWL) and South Western Escarpment (SWE) (Van Buskirk and Araia, 1994). The North Western Lowlands (NWL) is a wide semi-arid area over the western parts of the country bordering Sudan. It is characterised by hot and dry climate. It receives its annual rainfall, though small, mainly from the major rainy season (summer rain) and this rainfall is spread usually between July and August. The annual average rainfall is generally below and in some parts much below 400mm. The South Western Lowlands and Hills (SWL) are located south of the North Western Lowlands of the country. It has also a unimodal summer rainfall. Hot temperature but wet summer is the main feature of this sub-climatic zone. Over the rest of the year it is mainly dry and hot. The large rainy season spread between June and September and the average annual rainfall is roughly between 400 and 700mm. It is one of areas of interest for mechanised agricultural activities. The South Western Escarpment (SWE) is the area bordering the southern and central highlands with the western lowlands. This sub-climatic zone has mainly a unimodal summer rainfall. However, due to topographic enhancement it also receives a little rainfall in spring season as well. The average annual rainfall is not significantly different from that of the South Western Lowlands and Hills.

The highland area is divided into three sub-climatic zones: the southern part of the Central Highlands (CHS), northern part of the Central Highlands (CHN) and Northern Highlands (NH) (Van Buskirk and Araia, 1994). The Central Highlands (i.e. southern (CHS) and northern (CHN) parts of the Central Highlands) is a relatively wet region that receives its annual rainfall from both summer and spring rainy seasons. During Autumn and Winter it also gets some rainfall. The summer rainfall, its main rainy season, normally spreads throughout June to early September. The temperature over this sub-climatic zone is generally mild. The summer rainfall over the Northern Highlands (NH) is less in magnitude and highly variable as compared to the central. In addition to the summer season, the northern highlands also get winter rainfall due to penetration of mid-latitude frontal lows. The annual average rainfall varies between 100 and 500mm.

The Eastern Escarpment is a transition between the highlands and the eastern lowlands. South Eastern Escarpment (SEE), Central Eastern Escarpment (CEE) and North Eastern Escarpment (NEE) classifies the Eastern Escarpment (Van Buskirk and Araia, 1994). The South Eastern Escarpment is a dry and hot area with its average annual rainfall roughly ranges between 100 and 400mm. The Central Eastern Escarpment is the wettest part as well as green belt of the country. It receives rainfall almost the year round because of its unique topography and location. Generally it receives an average annual rainfall of over 1000mm. The North Eastern Escarpment gets its annual rain mainly from winter rainfall. It also receives small amount of rainfall during summer. The amount and distribution of rainfall over this area is much less than that of the Central Eastern Escarpment. Eastern Lowland is sub-divided in to North Eastern Lowlands (NEL), and South Eastern Lowlands (SEL). The two sub-climatic zones are characterised by hot, dry and humid coastal climate. The southern part is particularly the most arid zone in the country. The annual average rainfall is generally less than 200mm over the northern and less than 150mmover the southern part.

 

3. Rainfall Distributions and Mechanisms
1. Autumn Season

Autumn is a transition between the long-rainy season and the winter rainy season ("Kiremti Bahri") of the coastal area and eastern escarpment. During this season in most parts of Eritrea dry and cold weather prevails. At times summer rainfall mechanisms, tropical cyclone in the northern Indian Ocean and their interaction within the midlatitude systems provide short-lived rainfall over the country.

In this season the lower tropospheric flow is characterised by the interplay between the Arabian Peninsula and Sahara Highs. This result in northerly and northeasterly winds of dry continental air mass originated from Sahara and Arabian Peninsula, respectively. The Sahara and Arabian Highs are the extensions of the Azores and Siberian Highs, respectively. Over mid troposphere Northern Hemisphere subtropical high-pressure cells and their associated ridges characterise the flow over the country. In the upper troposphere the flow is mainly zonal westerly.

Fig. 2.5 Mean sea level pressure (mb) for October (Source: Tesfaye, 1982).

 

 

 

 

 

 

 

 

During this season tropical disturbances or cyclone form over northern Indian Ocean and Arabian Sea and these tropical disturbances occasionally have their tracks due north via Gulf of Aden. As they travel northwards they produce short-lived rainfall over some parts of the highlands, eastern escarpments and coastal areas. Thus, the Autumn wet spell over coastal plain, eastern escarpments and sometimes over the adjoining highlands are generally ascribed to the interaction between mid-latitude frontal systems and tropical systems.

 

2. Winter or "Kiremti Bahri" Season

The winter season is generally cold over most parts of the country. Fog and dew are common feature over the highlands and a fall in minimum temperature due to radiational cooling and / or advection of cold air from the winter hemisphere is also a prevalent feature in most parts of the country. This is a rainy season for the eastern lowland (coastal areas) and eastern escarpment. The eastern escarpment, coastal areas and some times the adjoining highlands are characterised by stratified low cloud.

In this season, like the autumn season, the lower tropospheric flow is influenced by the interplay between the Arabian Peninsula and Sahara Highs. As a result dry continental northerly and northeasterly winds from Sahara and Arabian Peninsula, respectively prevails all over the country. The middle and upper tropospheric flow is also generally similar to that of the autumn season. However, in winter season due to the intensification, eastward movement and / or southward shift of the mid latitude low pressure system over Mediterranean, the Arabian high pressure cell or its associated ridge is pushed either to the east or south towards north Indian Ocean. The high or ridge over northern Indian Ocean then generates south-easterly winds toward Eritrea and provide some parts of the country with moisture. The eastward movement of the mid-latitude low-pressure system and the protrusion of its trough towards south give rise to the development of high-pressure cell or ridge over Egypt region. Associated with Egypt high-pressure cell or ridge cold northwesterly winds flow southwards along the Red Sea and converge over the central Red Sea with the south-easterly winds originated from north Indian Ocean.

The line of convergence between these two air masses is called Red Sea Convergence Zone (RSCZ) (Pedgley 1966). The warm tropical southeasterly airmass rises over the cold mid latitude northwestely airmass and usually results in formation of stratified low cloud and at times convective cloud over the central and northern Red Sea coasts. As the availability of moisture over the lower troposphere becomes greater a wet spell occurs over coastal plain and over an extended areas of the eastern escarpment.

 

Fig. 2.6 Mean sea level pressure (mb) for January (Source: Tesfaye, 1982).

 

 

 

 

 

 

 

 

 

3. Spring Season or "Akeza"

This is a period of short rains for the highlands. The adjoining central eastern escarpment also gets some parts of its annual rainfall from this season. The season alternates between dry and wet spells over the highlands and central eastern escarpment. The western and eastern lowland remains dry and hot.

During a wet spell, the low tropospheric circulation is characterised by the protrusion of a trough from the east and northeastward moving mid-latitude families of frontal lows. The protrusion occurs when these lows are strong. As the result of this, the Arabian and Sahara highs weaken or are displaced from their position. With the displacement of the Arabian high or its associated ridge towards north Indian Ocean southeasterly moist winds generated by this high prevail over most parts of the highlands. In line with this, in the middle and upper troposphere westerly trough or subtropical westerly jet stream penetrates towards the region resulting in the southwesterly jet speed wind across the country. The lower level moisture convergence and upper level favourable diverging environment lifts the moist airmass and give rise to convective wet spell over the highlands. Orographic lifting and thermodynamic instability due to warm lower tropospheric flow and cold upper level westerlies enhance the spring rainfall.

As the mid latitude frontal low pressure decays a dry spell prevails over the country. Then the Sahara and Arabian Peninsula ridges or high-pressure cells control the flow over the lower troposphere. Moreover, the mid-and upper-trpospheric flow becomes zonal westerly or subtropical high. This condition will continue until another family of mid-latitude frontal lows evolve and initiate another wet spell.

Fig. 2.7 Mean sea level pressure (mb) for April (Source: Tesfaye, 1982).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Summer Season or "Kiremti"

"Kiremti" or summer rainy season is the main rainy season for Eritrea. It covers a wide area of the country and spreads mainly through June to September. The normal onset of the rainy season starts during mid to late June over the southern half of the country and proceeds with time towards north. The northward movement of the ITCZ as the Sun moves northward control the movement of the rain belt. The withdrawal of the rainy season occurs as the ITCZ retreats southward and this normally starts from the northern tip of the country during late August or early September and goes southward with time. The highlands, western lowlands and parts of the eastern escarpments are parts of the country that benefit rainfall during this season. The rainfall is mainly convective in nature. The variability of summer rainfall is high over all places and this is true in the other rainy seasons, as well. The country is frequently affected by late onset, early withdrawal and prolonged dry-spells within the season or confinement of rain belt within particular places. This variability greatly affects agriculture activities on which most of the people depends for their lives.

Fig. 2.8 Mean Period of On-Set and Cessation of large Rainy Season over Eritrea (Source: Meteorological

Map of Ethiopia, 1979, National Meteorological Services of Ethiopia)

 

 

 

 

 

 

 

 

 

 

 

 

During this season the lower tropospheric flow is controlled by Muscarine and South Atlantic high pressure cells located over South Indian Ocean and South Atlantic Ocean respectively, heat low over Arabian Peninsula and Sudan, and the Inter Tropical Convergence Zone (ITCZ). In addition to the ITCZ, a convergence line between the moist southerly and dry northerly winds, there is also a secondary convergence line between the moist and warm cross-equatorial monsoon flows originated from South Atlantic and Muscarine Highs. In the tropics this convergence line is called Congo Air Boundary (CAB) and is generally located south of the ITCZ. The intensity of the high-pressure cells influences its daily oscillation. It oscillates between southeast and northwest when the South Atlantic High and Muscarine High are stronger, respectively. Due to the monsoonal flow most parts of the summer-rain benefiting parts of the country are generally controlled by southwesterly or northwesterly winds. Thus, it seems that the South Atlantic Ocean is the main source of moisture for summer rainfall over most parts of the country. Northeasterly dry and continental wind is a prevalent flow during dry spell within the season.

Fig. 2.9 Mean Surface Flow Patterns and Locations of Discontinuities in the lower tropospheric

flow (Source:GARP Publication Series No. 21)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Due to strong solar heating in the Northern Hemisphere easterly thermal winds established all over the region and this results in the development of jet speed wind in the easterly in the upper troposphere. This jet is Tropical Easterly Jet (TEJ) and originates around Vietnam and extends across Africa. It is roughly located at about 15N and 100mb level. Strong upper level divergence associated with this jet give rise to wide-range of mass ascent in the lower troposphere along the ITCZ and the secondary convergence line. Therefore, the lower troposphere monsoonal convergence along the ITCZ and secondary convergence line and its associated moisture together with the upper troposphere divergence due to Tropical Easterly Jet provides a favourably mechanisms for the large rainy season of the country.

At times, due to the passage of the extra-tropical frontal low pressure systems in the southern hemisphere the South Atlantic High and / or the Muscarine high are displaced from their mean position. This leads to the weakening and / or displacement of the ITCZ and the secondary convergence line and thereby creates a dry spell within the season. The duration of the dry spell depends on the frequency of the family of the extra-tropical frontal systems of the Southern Hemisphere. This factor determines the interannual variability of the summer rainfall of the country. Though the effect is not yet studied, El Nino and Southern Oscillation (ENSO) also seem to play a role in determining the interannual variability of the climate of Eritrea.

Usually, as seen from satellite imageries cloud development begins over eastern escarpment or Yemen highlands. In line with the direction of the Tropical Easterly Jet Stream, the cloud moves westwards providing afternoon and night-time summer thundery shower over the highlands and western lowlands, respectively. The Yemen highground storm some times migrates towards the eastern coastal area and provides a significant amount of rainfall.

 

 

 

 

 

Chapter 3 Satellite and Satellite Based Rainfall Estimation Techniques

 

 

 

 

 

 

 

Chapter 3

 

 

2. Satellite and Satellite Based Rainfall Estimation Techniques

 

 

1. Rainfall and Rainfall Measurements

Rainfall is the main source of water that is most vital for human life. Thus, rainfall studies are essential in order to understand the supply and demand of water. Precipitation varies in its frequency, duration, intensity and spatial distribution and hence requires accurate observations (Barrett and Martin, 1981). Tropical rainfall is mainly convective and thus it is more localized and its spatial and temporal distribution as well as the intensity of rainfall is highly variable. The highly variable rainfall in tropics directly and / or indirectly affects different socioeconomic sectors namely agriculture, water resources, transport, construction, pest monitoring and so on. Therefore, it is essential to measure area rainfall on real time basis in order to see the influence of the variable rainfall on such sectors. Different instruments are used to measure and / or estimate rainfall over a place and these are discussed in the following sections.

 

1. Raingauges

A raingauge is a cylindrical funnel with a graduated cylinder used for collecting and measuring rainfall at a point. It is widely used standard measuring device. The measurement is read once every day and this gives a total rain fall over a place during 24 hours of time. The raingauge has the following advantages and disadvantages:

Advatanges:

1. It is cheap and easy to maintain and read;
2. Gauge data are available for many years and hence it is possible to do climatological analysis using long period gauge data; and
3. Comparison between gauge data from different region is possible.

Disadvantages:

1. It measures point data. Thus, even having a high density of gauge network area estimate of rainfall with reasonable accuracy is difficult to achieve. Moreover, it is impractical and not-cost effective to have a dense network that can measure the highly variable spatial distribution of rainfall like that in tropics.
2. Since gauges are read once every day to get real time information they should be located in places where there is easy access for an observer. However, there are remote areas of interest that are difficult to be accessed every day. Therefore, gauge networks can not cover all area of interest to make a real time observation.
3. Source of errors in the reading can easily be occurred due to:

1. Airflow;
2. Unrepresentative orientation and exposure of the gauge;
3. Human Observation and transmission; and
4. Evaporation from within the cylinder; gauge leaks and overflow.

1. Some times there might be time delay in getting the gauge data due to communication problem between the observer and the main center

Thus, the above limitations lead to the use of radar and satellite estimation that augment the raingauge data.

1. Radar

Radar is used to estimate rainfall over a given area by observing the back-scatter of electromagnetic radiation from liquid water drops. Radar has an advantage over raingauge for providing a spatially continuous image (Barrett and Martin, 1981).

Advantages of Radar:

1. With Radar real time data acquisition is possible – the data can be viewed every few hours;
2. Radar provides area estimate of rainfall which can not be attained by rain gauge;
3. The estimated rainfall from radar is computerized thus ready for further analysis; and
4. By animating the images it is easy to monitor the development, progress and motion of the rain producing systems.

Disadvantages of Radar:

1. It is expensive and requires sophisticated technical and engineering support;
2. Buildings, nearby weathers, mountains etc. contaminate the radar signal and thereby the rainfall estimate;
3. Low level precipitation may be overlooked by radar signal;
4. Since radar covers a limited area many radar are needed to cover a large area of interest; and
5. Needs calibration with ground measured data

However, satellite is inexpensive, covers more area and also does not require sophisticated technical and engineering support. Therefore, for Africa use of satellite is more advantageous than radar.

1. Satellite

A Satellite is a spacecraft that orbits the earth and returns images of the earth and the atmosphere back to the receiving station on the ground. Satellites are used to estimate rainfall using radiation signals reflected or emitted from the ground and atmosphere and observed by it. The following are advantages and disadvantages of satellite based area rainfall estimation.

Advantages:

1. Real time estimate is possible and once the satellite is in orbit it is inexpensive;
2. Provide a large area coverage;
3. Area estimate is possible; and
4. Animation of the images to observe the development, progress and motion of the weather system is possible.

Disadvantages:

1. Needs calibration with ground measured data;
2. Since the estimates are indirect contamination (over estimate and/or underestimate) occurs; and
3. Different techniques of rainfall estimations have their own limitations that are to be discussed later.

1. Meteorological Satellite
1. History

Understanding the importance of observing weather from space Verner Sumoi and colleagues at the University of Wisconsin developed the first successful meteorological satellite that was launched on 13 October 1959. This satellite used a Suomi radiometer and returned coarse maps of reflected solar radiation from the earth surface and infrared radiation emitted by the earth (Kidder and Vonder Haar, 1995). On 1 April 1960 a first satellite completely dedicated to meteorological purpose was launched and TIROS 1 (Television and Infrared Observational Satellite) was the 22^nd successfully launched satellite. TIROS 1, had a lifetime of 79-day, was the first satellite that returned an image of the earth with its weather systems as a whole. Since then several technological improvements were made in the TIROS series and eventually the present standard TIROS N series is reached.

The development of Application Technology Satellite (ATS 1) by Verner Suomi and Robert Parent at the University of Wisconsin was a another leap forward in satellite meteorology (Kidder and Vonder Haar, 1995). The ATS made possible rapid imaging and watching of weather systems as they develop, move and decay – important information for forecasting. This satellite was launched into a geostationary orbit and carried a Spin Scan Cloud Camera for producing visible images of the earth. Synchronous Meteorological Satellites 1 (SMS 1) was the first generation of semi-operational geostationary satellite that was launched in 1974. The second series of SMS (i.e. SMS 2) had a Data Collection System (DCS) instrument used to relay meteorological and other data transmitted from ground-based instruments. DCS made possible to relay meteorological information from remote area to a central receiving station. SMS and the succeeding GOES have both an infrared and visible radiometer which enabled them to return both visible and infrared images of the earth and its atmosphere. Geostationary Operational Environmental Satellite 1 (GOES 1) was the first operational geostationary satellite that was launched in 1975. In the late 70s Japan’s Geostationary Meteorological Satellite 1 (GMS 1) and European Space Agency’s Meteosat 1 were launched. The Meteosat 1 in addition to the visible and infrared had a third channel of water vapour.

2. Polar Orbiting Satellites

Polar orbiting satellites are launched into sun-synchronous orbits at an altitude of about 800km.

The sun-synchronous orbit of the polar orbiting satellite enable them to observe the signal at each location with the sun always be in the same place in the sky (Houghton and Taylor, 1973). For example, if the satellite crosses a certain place at midday when it goes to the northern pole then as it goes to the southern pole it re-crosses the place at midnight. The satellites have a period of about 100 minutes i.e. they take about 100 minutes to complete an orbit and scan the earth’s surface in about 24 hours. The METEOR of the former Soviet Union and the US TIROS are polar orbiting satellites and of which the TIROS (NOAA Series) are the most widely used. India also launched two polar orbiters: Bhaskara 1 and Bhaskara 2 in 1979 and 1981, respectively.

Polar orbiting satellites are essential to provide global and hemispherical image of the weather (Houghton and Taylor, 1973). However, images from polar orbiting satellite are obtained only once or twice per day, and hence for continuous monitoring of the weather it becomes difficult to rely only on polar orbiting satellites. On the other hand, because of their low orbits the spatial resolution obtained from polar orbiting is higher than the geostationary one’s (i.e. polar orbiters observe a lot of detail information than the geostationary satellites).

The TIROS series satellites have a number of sensors (instruments) that are used for meteorological and non-meteorological purposes (Kidder and Vonder Haar, 1995). These include Advance Very High Resolution Radiometer (AVHRR), High Resolution Infrared Radiation Sounder (HIRS), Microwave Sounding Unit (MSU), Stratospheric Sounding Unit (SSU), Solar Backscatter Ultraviolet Radiometer (SBUV), Earth Radiation Budget Experiment (ERBE), Space Environment Monitor (SEM), Data Collection System (DCS), and Search And Rescue (SAR). Of these only AVHRR and DCS are directly related to meteorological purposes.

 

3. Geostationary Satellites

Geostationary satellites orbit the earth at about 36000km and have a period of 24 hours to complete the orbit. Their orbit enables the satellites to remain at the same point in the sky with respect to the ground and watch the same parts of the earth with a high temporal resolution. The high temporal resolution of the geostationary satellites enables them to carryout continuous monitoring of the weather. On the other hand, the high orbit of the satellites makes them have low spatial resolutions. There are a number of geostationary satellites dedicated to view particular area of interest in the world.

1. Japanese National Space Development Agency (NASDA) and the Japanese Meteorological Agency launch Geostationary Meteorological Satellite (GMS). It is located at 140^o east. GMS has a spin scan radiometer that provides images of the earth and the atmosphere in visible and infra-red wavelength of the electromagnetic spectrum.
2. INSAT is a geostationary satellite launched by India. It is located above 74^o east. It is the first geostaionary satellite with no-spinning radiometer, instead their instrument always points towards Earth like those on the low Earth orbiters. The low earth orbiters observe from many angles however, other geostationary satellites observe each point from one angle only. INSAT provides visible and infra-red images of the earth and the atmosphere.
3. NOAA launched a series of Geostaionary Operational Environmental Satellite (GOES). There are two GOES satellites: GOES-East and GOES-West that are located over 75^o west and 135^o west, respectively.
4. European Space Agency launched METEOSAT. It is located over 0^o latitude and 0^o longitude above the earth surface. Its positions are suitable for watching a continent of Africa. A spin Scan Radiometer is the meteorological instrument on meteosat that enables it to return images of the earth and atmosphere in the Visible (0.4-1.1mm) and Thermal Infra-red (10.5-12.5mm) and Water vapour (5.5-7.1mm). East-west optical scanning is achieved by the rotation of the satellite at the rate of 100rpm, while the north-south optical scanning is done by a scan mirror that moves in 192 mrad steps. Thus, full-disk hemispherical image is obtained from the east-west and north-south optical scanning.

1. Rainfall Estimation Techniques
1. Background

Different methods are available for estimating area rainfall using images of visible (wavelength between 0.4 and 0.7mm) and infrared (wavelength between 10.5 and 12.5mm) electromagnetic radiation from geostationary satellites. The visible channel measures the short wave radiation backscattered by the atmosphere and the earth. This channel gives the albedo of the reflecting body and high brightness implies a highly reflecting cloud. The high cloud brightness in turn is related to the cloud optical thickness and liquid water content. However, this relation is valid only for cloud thickness less than 700m beyond which the relation saturates and there is little change in the cloud albedo (Twomey et al., 1967). The infrared channel measures thermal radiation emitted by cloud (assumed to be a perfect emitter) and this is related to the temperature of the emitting cloud by the Planck’s radiation law. On this approach the height of the cloud is inferred from the temperature of the cloud top that is obtained from satellite infrared observation. Thus, cold cloud is assumed to be deep and rain giving. Therefore, high brightness in the visible channel and low temperature in the infrared channel imply large cloud thickness and high cloud top respectively. These in turn imply greater probability of rain. Therefore, the brightness and / or temperature of precipitating cloud are an indirect measure of convective rainfall intensity.

Though not yet developed for real time daily operational application there is also a microwave methods of rainfall estimation that uses microwave sensors. This technique, unlike the visible and infrared techniques, is a direct way of estimating rainfall.

Estimation of rainfall from satellite over Africa is useful in order to augment the rainfall data obtained from relatively sparse raingauge network in the region. Moreover, the real time satellite estimation also solves the delay of information on rainfall that might be caused by ineffective means of communication from out-station to the central body. Some of rainfall estimating techniques will be discussed in the following sub-sections. The techniques that will be discussed in this study are Microwave, CPC, OSTROM and TAMSAT and most of them are relevant to Eritrea type of climate.

 

 

2. Microwave Rainfall Estimation Technique

Microwave radiation (3 – 300GHz or 10 – 0.1 cm) may be absorbed, reflected or scattered by water and ice hydrometeors. The strong interaction of the water drops and ice crystals with microwave radiation makes the microwave rainfall estimation technique more direct and physically based than the infrared and visible techniques particularly over ocean surfaces. The technique is based on the fact that microwave radiation at frequencies below 30GHz are absorbed / emitted by liquid raindrops while higher frequencies are scattered by ice crystals and raindrops (Spencer et al., 1997).

Microwave radiation from the surface depends on the angle of view, the surface emissivity and the frequency of the radiation being detected. Ocean has a greater reflectivity and thus lower emissivity than land surface. Moreover, the emissivity of ocean surfaces is almost constant while changes in land surface and soil moisture make the emissivity of land surfaces highly variable. Therefore, microwave rainfall estimation can be carriedout over ocean surfaces without problem, however, the estimation is affected over lands surfaces (Morland et al., 1997). Consequently, the direct relationship (i.e. the physical algorithm) between the microwave radiation and rainfall becomes impractical over land surfaces. Instead, over land surfaces the microwave rainfall estimation technique depends, like the visible and infrared techniques, on an empirical and statistical relationship. The microwave rainfall estimating technique has the following drawbacks that make it difficult for continuous monitoring of variable rainfall: low temporal resolution (i.e. 1 – 2 images per day) and spatial resolution (at least 10km) (Barret and Beaumont, 1994). Therefore, it is not useful technique for highly variable rainfall of Eritrea.

 

 

3. CPC Rainfall Estimation Technique

The CPC technique is a technique developed for estimating accumulated rainfall using Meteosat satellite data, raingauge data obtained from Global Telecommunication System (GTS), model analysis of wind and relative humidity and orographic feature (Herman et al, 1997). The technique was developed for drought monitoring purpose by United States Agency for International Development (USAID) Famine Early Warning System (FEWS). It is capable of estimating rainfall from convective (cold) as well as stratified (warm) clouds. This technique is discussed here because of its importance in estimating rainfall from warm cloud in Eritrea.

GOES Precipitation Index (GPI) is an algorithm developed to estimate accumulated rainfall for ten-day period from convective cloud using cold cloud tops duration over a region (Herman et al, 1997). In the GPI algorithm 3mm of precipitation corresponds for each hour that cloud top temperature are measured to be less than 235K. The raingauge data obtained every six hours from GTS is summed every 24 hours and then every ten-day is compared with the GPI estimated rainfall. A bias adjustment to the GPI estimate is then done empirically using statistical estimation by fitting the GPI estimates to raingauge data. Then this improved GPI algorithm is called CPC (Climate Prediction Center) technique and is used for estimation of convective rainfall.

However, the CPC technique still has an overestimate and underestimate biases over some cases. It overestimates rainfall particularly over a region where there is persistence of cirrus cloud (cloud that is cold but not thick enough to precipitate). On the other hand, underestimate by the algorithm is common in a region where there is orographic precipitation and precipitation from warm clouds. Such warm cloud precipitation is common particularly over coastal and mountainous region of Africa continent. Therefore, some modification was done to the CPC technique in order to estimate precipitation from warm and stratiform cloud.

When there is moisture and favorable low-level wind moist air can rise and condense to provide precipitation from warm cloud (i.e. clouds with cloud top temperature roughly ranges between 275-235K). For estimating precipitation from warm cloud data on low-level wind direction, relative humidity and the terrain slope are used. Wind vector and relative humidity are obtained from model analysis for the 00, 06, 12 and 18 UTC and are combined with the slope of the terrain, that is computed using finite difference method, in the following way.

At every half-hour interval dot product of the terrain slope and wind is computed. The scalar product of the surface wind vector (u(x,y),v(x,y)) and the horizontal gradient of orography gradient [h(x,y)] i.e.



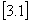
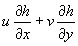
is approximated by finite differences centered at the grid points. The dot product values are then interpolated to a grid with the same resolution as the Meteosat data and finally it is multiplied by the analyzed surface relative humidity in order to incorporate the orographic lift of low-level moisture. Every half-hour for each grid point, where the cloud top temperatures ranges from 235 to 275K, the product of the surface relative humidity and the dot product is stored. The product is then summed for ten-day period and calibrated with the raingauge values to be used for estimation of rainfall from warm cloud.

A calibration for estimation of rainfall by dot product technique was carriedout over parts of Africa using data for two-month period of 20 May to 19 July 1995 (Herman et al, 1997). The selected sites for the calibration were areas where there was no cold cloud duration during that period and precipitation was entirely orographic. The relationship between rainfall and relative humidity times dot product of orography and wind (Fig 3.2) applied uniformly over the whole continent of Africa.

Fig. 3.2 Calibration relationship for warm cloud precipitation algorithm. Rainfall (mm) vs dot product

times relative humidity (ms^-1) (Herman et al, 1997).

 

 

 

 

 

 

 

Therefore, the CPC (Climate Prediction Center) of the National Centers for Environmental Prediction (NCEP) combined the bias adjusted GPI algorithm with the dot product of the wind and orography multiplied by the relative humidity to estimate total accumulated precipitation from both convective and stratiform clouds. The validation of the CPC combined estimated precipitation with raingauge data indicated that there is relatively high accuracy over Sahel region of Africa.

The CPC technique is advantageous in that it can estimate precipitation from both cold and warm clouds. In Eritrea winter rainfall over the coastal areas and the eastern escarpment is mainly from warm cloud. Moreover, during summer warm cloud rainfall occurs over the highlands and eastern escarpment when there is enough moisture and favorable low-level wind flow. Therefore, the CPC technique is useful for Eritrea in estimating rainfall from warm cloud. Though it is important to calibrate using CPC technique for estimating warm cloud rainfall in Eritrea, time allowed for this study was not enough to do the calibration for Eritrea.

The CPC technique of estimating rainfall from cold cloud is calibrated against a contemporaneous gauge data rather than historical data. Therefore for calibration we need enough real-time raingauge data on ten-day basis. However, in Eritrea the number of stations that report raingauge data on ten-day basis are roughly 40 and these may not include all areas of interest and also may not be sufficient in number to do the calibration.

 

4. ORSTOM Rainfall Estimation Technique

The ORSTOM technique uses ground surface temperature (Ts) obtained from Meteosat images for estimating rainfall (Guillot, 1995). It was developed by the Lannion Centre De Meteorologie Spatiale (CMS) and tested in west Africa. The technique is discussed here because of the similarity of the climate of west Africa to that of Eritrea. The approach depends on the relationship between ground surface temperature (Ts) and pluviometry and this is based upon the following two balances (Guillot, 1995): energy balance that links sensible heat flow to evapotranspiration and water balance that links evaporation to rainfall. The sensible heat (fs) is also related to the ground surface temperature (Ts) by the following linear relationship.

fs = rCph(Ts – Ta) [3.2]

where r is voluminal mass of the air, Cp is specific heat of the air, h is exchange coefficient,

Ts is ground surface temperature and Ta is temperature of the air.

The technique is based upon the effect of the previous rainfall on the ground surface temperature. It was found that there is an inverse relation between ground surface temperature Ts and the corresponding rainfall totals S P of the same period. However, there may be local climatic factors that results in ground surface temperature gradient across the region of consideration that is independent of the pluviometry. This may result in a south-north and west-east temperature gradient across the considered region. Therefore, before the first rain examination of the ground surface temperature is required in order to identify its variation due to local climatic factors. In that case in order to take the local climatic factors across the considered region into account Ts is reduced by DTa = Ta – To, where To is the temperature of the air at a reference station. Therefore, the above relation is modified to a relation between rainfall totals S P and sum of ground surface temperature (Ts) minus temperature gradient of the air (DTa) i.e. S (Ts – DTa).

In Senegal a study of the relation between rainfall totals and sum of ground surface temperature minus temperature gradient of the air was carriedout (Fig. 3.3) (Guillot, 1995). The examination of the ground surface temperature showed that before the first rain there was a 3^o to 8^oC south-north or west-east gradient. The negative linear correlation between the rainfall totals and the mean temperature Ts - DTa from June onwards indicated that the variable S (Ts – DTa) explained about 73% of variation of rainfall totals from end of July and for the three consecutive years period of 1984 to 1986 (Guillot, 1995). The result obtained from that study and the comparison with rainfall computed by kriging ground data showed that:

1. except at the beginning of the season there is a greater accuracy obtained by this relation in a region where there is low density of raingauge; and
2. there is an equal precision in the regions where there is a medium density of raingauge.

Fig. 3.3 Rainfall correlation – Sum of Surface Temperature Ts – Temperature gradient of the air DTa,

Combining both the ground surface temperature and the cold top cloud frequency techniques resulted in an improved accuracy of the estimations (Fig. 3.4) (Guillot, 1995). The combined technique was done over Niger and a positive correlation between the combined parameters and estimated rainfall was obtained. The cold top cloud occurrences were obtained by counting the number of clouds colder than –40^oC and the cold cloud frequency was then calculated using the relationship: number of favorable cases / number of possible cases. However, the combined methods underestimated rainfall in the wetter regions and overestimated over the drier regions of Niger, and these were corrected by using temperature of surface air obtained either from the network or analyzed fields from the European Center for Medium Range Weather Forecasting (ECMRWF) at Reading. Thus, the relationship becomes:

Pe (estimated rainfall) = aOc + b (Ts – Ta) + cte [3.3]

Where Oc is cold top cloud frequency, Ts is ground surface temperature, Ta is air temperature, and a and b are constants.

1995). r= correlation coefficient; T^omax: method using surface temperature; Oc: method using cold top

As indicated by correlation coefficient (r), the ORSTOM technique has a greater accuracy. However, it has the following drawbacks that may make its calibration for Eritrea not easy:

1. It needs some surface data (e.g. temperature); and
2. It is calibrated against contemporaneous gauge data

1. TAMSAT Rainfall Estimation Technique

The TAMSAT group in the University of Reading developed the technique from the GOES Precipitation Index (GPI) for estimation of rainfall over Africa. Unlike the CPC and ORSTOM techniques, TAMSAT technique is entirely pre-calibrated i.e. it is calibrated against historical rather than contemporaneous gauge data.

The TAMSAT (Tropical Application of Meteorological SATellite) rainfall estimation technique uses half-hourly or hourly infrared images from Meteosat satellite. The use of a single infrared sensor made the TAMSAT techniques simpler to automate, otherwise the technique would have been difficult for automatic operational procedures. The technique has the following assumptions:

1. Convective clouds are the main source of rain;
2. The convective clouds gives out rain if and only if they reached a certain threshold height i.e. if they are deep enough;
3. The threshold height, above which the cloud gives out rain and below which it doesn’t, corresponds to certain cloud top temperature and thus it is expressed in terms of the cloud top temperature; and
4. The amount of rainfall over a place is directly proportional to the duration of the convective clouds with the top temperature below the threshold temperature. The duration of time is called Cold Cloud Duration (CCD).

In TAMSAT approach raingauge values are related to the CCD values using the following linear relationship:

Where R is rainfall, CCD is Cold Cloud Duration value and a₁ and a_o are constants to be determine by comparison of CCD images with raingauge data.

• Procedures of the Techniques

1. Generate CCD images at different temperature thresholds;
2. Determine an optimum threshold temperature for each calibration zones;
3. Determine calibration parameters a_o and a₁ for each calibration zone; and then
4. Using the CCD / rainfall relationship formula estimate rainfall

Determination of optimum temperature threshold for each calibration zone is done using contingency table (details in page 39).

Since the relation between rainfall and CCD is stochastic, a substantial amount of averaging is needed to give a meaningful calibration (Grimes et al, 1993). The following two different approaches for determining the calibration parameters (a_o and a₁) and thereby estimating rainfall is described:

1. Regression of median gauge against mid-class CCD: In this approach days are classified according to CCD value. Regression of median gauge in each class against mid-class CCD is used for the calibration. The approach of using median as a representative rainfall value is to eliminate the influence of outliers on the calibration. Here only non-zero CCD values are used in calculating the calibration parameters a_o and a₁. The approach is useful for drought monitoring purposes.
2. Regression of daily mean gauge values against daily mean CCD for pixel: The approach assumes that gauge pixels are representative of the rainfall / CCD relationship for the catchment area. This approach is useful for hydrological purposes.

Of the above calibration approaches the first one i.e. regression of median rainfall against mid-class CCD is used in the calibration of this study. This approach which is useful for drought monitoring purpose is relevant to Eritrea.

• Limitations of the Technique

1. Spatial variation of rainfall: The method estimates rainfall using the cloud top temperature without looking beneath the cloud. However, the intensity of rainfall may show spatial variation beneath the cloud and thus the technique does not consider the actual spatial variation of rainfall intensity beneath the cloud. Thus, the technique is useful for getting average rainfall over an extended area and period of time rather than detail information over small area and short period of time.
2. Contamination by Low clouds: In some places and times low clouds produce rainfall and in that case the approach that assumes rain occurs only from convective cloud, fails to work. When there is rain from low cloud, the technique says no rain.
3. Contamination by cirrus clouds: Cirrus cloud appears in the satellite as very cold cloud and thus the technique expects rainfall from such. However, the cirrus cloud is not deep enough to give rainfall. Therefore, the techniques indicate rainfall while there is no rain.
4. Different calibration for different regions and months: In the approach local calibration is needed and also the calibration differs from month to month.

Because it is pre-calibrated the TAMSAT technique has lesser accuracy than for example the ORSTOM technique. If the TAMSAT technique were calibrated against contemporaneous gauge data the accuracy would be greater. However, unlike the CPC and ORSTOM techniques in the TAMSAT technique the calibration can be carried out with more historical gauge data because these data are easily available than the real-time data.

In Eritrea for estimating rainfall from cold cloud the TAMSAT technique is appropriate because it is entirely pre-calibrated, automated and easy for operational applications. However, in order to estimate rainfall from warm and stratified clouds the use of CPC technique is highly recommended. Therefore, in the following chapters calibration was carriedout for Eritrea using TAMSAT technique.

1. Data Analysis and Results

 

1. Data availability and reliability

Eritrea has not yet established a national meteorological centre that is responsible, among other things, for standardizing meteorological instruments and stations as well as methods of observations within the country according to the established and recommended international standards. Thus, lack of one central responsible body results in decentralized meteorological stations and observations by various governmental organizations mainly Ministry of Agriculture, Meteorological Services of the Civil Aviation Department and Water Resource Department.

This decentralized approach resulted in:

1. Incompatible and non-uniform gauge type used within the country by various organizations and even within different stations of the same organization;
2. Non-standardized orientation and exposure of the gauge; and
3. Non-standard methods of observations.

Unlike those of the Ministry of Agriculture and the Meteorological Services, most of the stations under the Water Resource Departments are automatic and their readings are not collected on real-time basis. In this study the gauge data from the Ministry of Agriculture and Meteorological Services are used. The Cold Cloud Duration (CCD) data used is obtained from the Department of Meteorology of the University of Reading Data Archives and these include CCD with threshold temperatures of –30, -40, -50 and –60^oC. Ten-day cumulative CCD and rainfall from 1994 to 1997 are the data used in this study.

Most of the rainfall stations in the country are located over densely populated areas particularly over the highlands and southwestern lowlands of the country (Fig. 4.1). The non-uniform distribution of gauge over the country might be ascribed to the population distribution and agricultural and hydrological significance. The existing station network over the coastal areas, eastern escarpment and the northwestern lowlands are insufficient for this study. Moreover, the non-uniform and non-standard instruments, orientations, exposure and methods of observations within the country might make the accuracy and reliability of the data questionable. Thus, bearing in mind the accuracy and reliability of gauge data; the results should be used cautiously.

1. Data Analysis and Results

Cold Cloud Duration (CCD) at thresholds -30, -40, -50 and –60^oC are extracted from satellite image pixels for all available gauge rainfall stations in the country. In Excel all gauge data are imported and combined with the corresponding CCD values.

1. Determination of Best Threshold Temperature

Comparing CCD values at different thresholds with rain gauge data of the zone does the determination of best threshold temperature for each zone. As discussed in the preceding chapter, the optimum temperature threshold determination for each calibration zone is easily done using the following contingency table.

Where n₁₁ is the number of occasions having both gauge records and CCD values are zero,

n₁₂ is the number of occasions having gauge records zero but CCD values non-zero,

n₂₁ is the number of occasions having gauge records rainfall but CCD values is zero,

n₂₂ is the number of occasions having gauge records and CCD values are non-zero,

In n₁₁ and n₂₂ both gauge and satellite values agree each other but they disagree in n₁₂ and n₂₁. Thus the optimum temperature threshold is the one in which:

1. the number of occasions of agreement (n₁₁ + n₂₂ ) is much greater than the number of occasions of disagreements (n₁₂ + n₂₁) i.e. n₁₁ + n₂₂ >> n₁₂ + n₂₁; and
2. the disagreements at both ends are nearly balanced each other i.e. n_{12 @} n₂₁

Previous TAMSAT calibrations were done using the contingency table. However, in this analysis, instead of contingency table, accuracy and bias are calculated for each grid square and the optimum thresholds (high accuracy and low bias) for each grid square are then determined from the accuracy and bias analysis (Fig. 4.5 and Appendix 3). This new approach is used because the number of gauges (data points) used in this study is not sufficient to determine optimum threshold using contingency table approach.

In this study determination of best threshold is done in Excel. The data is organised in columns of country name, station, longitude, latitude, dekad, gauge value and CCD of different thresholds in separate columns (Table 4.1). This is done for each month from June to September. In order to see the station distribution gauge location is plotted as shown in Fig. 4.1. The region is gridded into one-by-one degree grid square (Fig. 4.2) and each grid cell is numbered starting from the topleft. Then for each station a grid cell number is assigned and the cell number for each station is included in separate column of the worksheet. Moreover, grid cell midpoint-longitude and -latitude are calculated and included in other columns of the worksheet.

Where 36 and 19 are the top-left longitude and latitude and 1 is the width of the grid square.

The analysis is done for each CCD threshold and any row with either missing rain gauge or CCD is deleted from the sheet. The data were sorted by station and then the sub-total rainfall and CCD of a particular month for the years 1994 to 1997 is calculated for each station. Each sheet contains data on Grid number, Longitude, Latitude, Date, Rainfall, CCD threshold, Grid cell number, Mid-longitude and –latitude of grid cell.

In order to identify the best CCD threshold temperature that discriminates rain from no-rain each CCD threshold temperature is classified into success, too warm and too cold. Successes (n₁₁ + n₂₂) are defined when there is no gauge rain and zero CCD (i.e. Rain=0 and CCD=0 for a particular gauge) or when there is rain and CCD (Rain>0 and CCD>0 for a particular gauge). Too Warm (n₁₂) means when there is CCD but no gauge rain (i.e. Rain = 0 and CCD > 0). Too Cold (n₂₁) means when there is rain but no CCD (i.e. Rain > 0 but CCD=0). Successes, too warm and too cold are calculated for all data points and each is given a value of either 1 or 0. For example, if the data point is success 1 is assigned in the success column and 0 is assigned in the too warm and too cold columns for that particular data point. Having done the above, the whole data is sorted by success and too warm in descending order and thereby classified into three classes (success, too warm and too cold) for plotting. Then a map that shows a distribution of successes, too warm and too cold is plotted for all months and different CCD thresholds (Fig. 4.3). Note that the gauge in figure 4.3 are outside Eritrea for the month of June. This is because for June northern Ethiopia gauges are also used.

The preceding figures show the distribution of successes, too warm and too cold by station. Identifying best CCD threshold with high accuracy (n₁₁+ n₂₂>> n₁₂+ n₂₁) and equal distribution of too warm and too cold (no bias in either end i.e. n_12@ n₂₁) was the aim of this analysis. However, from the above-congested figures it became difficult to identify such optimum threshold and thus the following further analysis was carriedout.

The distribution of successes, too warm and too cold is processed and plotted for each grid square rather than for each station. The data were sorted by grid number and then sub-total rainfall and CCD threshold temperature of a particular month for the years 1994 to 1997 was calculated for each grid number rather than station names. The sheet contains columns on grid number, successes, too warm, too cold, total sums of successes, too warm and too cold, accuracy, bias, mid-longitude and mid-latitude. Too warm (n₁₂) and too cold (n₂₁) were calculated for each grid number. The successes were divided into two: n₁₁ and n₂₂. Success of no rain and zero CCD (i.e. Rain=0 and CCD=0) is denoted by n₁₁ and success of rain and none-zero CCD (Rain>0 and CCD>0) by n₂₂. Accuracy and bias are then calculated as follows:

A high accuracy and low bias is considered to be a best CCD threshold that discriminates rain from no-rain. The accuracy is then classified into five different classes i.e. below 20%, 20-50%, 50-70%, 70-90%, and above 90% and on the other hand the bias is classified into three categories: cold bias (< -20%), no bias (-20% to +20%), and warm bias (>20%). The result obtained from this analysis is shown in the following figures. Therefore, from the accuracy and bias maps and graphs indicated in the following figures (fig. 4.4 and 4.5) optimum threshold is determined for each grid square.

1. Delineation of Constant Threshold Region (CTR)

Constant Threshold Region (CTR) is a region within which rainfall is assumed to be similar or homogeneous and thus the best temperature threshold and the calibration parameters (i.e. a_o and a₁) are the same.

The accuracy and bias maps and graphs plotted in the preceding figures (figures 4.4 and 4.5) became useful and easy in identifying the best threshold for each grid square and thereby in delineating the Constant Threshold Regions (CTR). For each grid square in figure 4.5 and appendix 3 an optimum threshold (high accuracy and low bias) is selected. Each grid square with the same optimum threshold is then identified and thus amalgamated to form a calibration zone or Constant Threshold Region (Figure 4.6). Eritrea falls into two constant threshold regions. The highlands, southwestern lowlands and parts of the eastern escarpment lie under a homogeneous constant threshold region while the northern tip of the country and the eastern lowlands (coastal areas) lie under different constant threshold region (Fig. 4.6). Due to unavailability of gauge over the northwestern lowlands calibration was not carriedout.

Fig. 4.6 Constant Threshold Region (CTR)

 

 

 

 

Fig. 4.6 Constant Threshold Region

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Determination of Calibration Coefficients

Regression of median gauge against mid-class CCD approach, that is useful for drought monitoring purposes, is used in the calibration. Days are classified according to CCD value and regression of median gauge in each class against mid-class CCD is used for the calibration. Only non-zero CCD values are used in calculating the calibration parameters a_o and a₁.

Determination of calibration coefficient and validation are done only for the Constant Threshold Region (CTR) that comprises the highlands, southwestern lowlands and parts of the eastern escarpment. For the other CTR that comprises the eastern lowlands and northern tip of the country the determination of calibration coefficient and validation are not done for the following reasons:

1. except occasional rain, summer is mainly dry; and
2. during summer large number of events over these regions is no-rain and this resulted in zero median gauge rainfall. The zero median gauges obtained in turn made the calibration process difficult.

The calibration coefficients for the highlands, southwestern lowlands and parts of the eastern escarpment are done in the following ways. For each month stations that belong to the same Constant Threshold Region (CTR) are sorted and separated from the others. About thirteen CCD class intervals are defined and the CCD class number 1 to 13 is assigned to each class. Mid class CCD is calculated and for each CCD data their corresponding CCD class is derived. Median rain and number of data are also calculated for each CCD class (Table 4.7). CCD = 0 is excluded from this data set because of the assumption that when CCD = 0 rainfall is assumed to be zero. Regression analysis between mid class CCD and median rain is done as follows:

Table 4.2 Sample of worksheet used for determination of calibration coefficient

Where x and y are mid class CCD and median rain, respectively and the sign < > indicates weighted means. The number of points in each class weights the mean. Thus, for the highlands, southwestern lowlands and parts of the eastern escarpment the slope (a₁) and the intercept (a_o) are shown in Table 4.8.

Therefore, the calibration equations for the southwestern lowlands, highlands and parts of the eastern escarpment are:

A scatter plot of mid class CCD against median rainfall is presented in Fig. 4.7. The observed linear relation and the R² shown in the regression analysis are reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment.

1. Estimation of Rainfall and Evaluation of Calibration

In order to identify areas where the calibration algorithms and thresholds are inappropriate or needs further refinements and also to assess the skill of the estimate it is useful to evaluate the calibration.

Finally, using the calibration equations (Equation 4.4) for the constant threshold region that comprises the highlands, southwestern lowlands and parts of the eastern escarpment estimated rain is calculated. Plots of the estimated rainfall against gauge value are shown in Fig. 4.8. The validation is not done using an independent data set, however; it is done with the same data that are used in the determination of calibration coefficient (1994 – 97data).

The estimated rain is more or less reasonably good over most parts of the calibration zone. The evaluation indicated that there is a reasonable agreement between the satellite estimate and gauge value in all considered months (June to September). In June, July, August, and September over 76%, 67%, 60% and 83% of the stations respectively the gap between the satellite estimate and gauge value is less than 10mm – and this is reasonably good. Generally, the disagreement (gap) between the satellite estimate and gauge values occurs mainly due to under-estimate. The under-estimate does not occur in a particular climatic region, so it is difficult to identify a particular region where the calibration is under estimating.

1. Discussion and Conclusions

 

 

1. Discussion
1. Climate and Rainfall Summary over the Calibration Zones

The calibration analysis is done for summer rainy season (June to September) which is the major rainy season for the highlands, southwestern lowlands and parts of the eastern escarpment. During normal years clouds usually develop over the eastern escarpment or its adjoining highlands and moves towards the western parts of the country. In line with that, the rain belt also move from the eastern parts of the country towards the west. During wet spells, low level moist southwesterly winds originated from Southern Hemisphere maritime high-pressure cells converge with the dry northerly winds along the InterTtropical Convergence Zone (ITCZ) (Fig. 2.8). Generally in a normal summer rainy season the highlands, parts of the eastern escarpment and southwestern lowlands receive more or less similar type of rainfall.

During the summer season, except occasional rain the northern tip of the country and the eastern lowlands (i.e. coastal areas) usually remain dry. Over the eastern lowlands wind generally descends towards lower altitude leaving it a rain shadow region. However, at times when big storm develops over the Yemen high ground it moves towards west and provides rain over the northern tip of the country and eastern lowlands. Thus, the rainfall over these climatic regions occurs when the rain-giving meteorological mechanisms are favourable in producing big storms over Yemen. Otherwise, frequent small storms over Yemen highlands give rain over Yemen and disappear without moving to the west and producing rain over eastern lowlands and northern tip of the country.

 

2. Definition of the Constant Threshold Region (CTR)

Based on the calibration analysis Eritrea falls into two Constant Threshold Regions (CTR): the first comprises the highlands, southwestern lowlands and parts of the eastern escarpment and the other comprises the eastern lowlands (coastal areas) and northern tip of the country. The calibration was not carried for the Northwestern Lowlands due to lack of gauge data. The separation into two constant threshold regions (CTR) can be explained in terms of the two different weather systems:

1. The rainfall over the eastern lowlands and northern tip of the country occurs when the rain-giving meteorological mechanisms are favourable to producing big storms over Yemen. Therefore, this constant threshold region, generally, receive occasional and similar type of rainfall from migration of big storms (i.e. deep clouds) from Yemen high ground. This is in agreement with the fact that they (the northern tip of the country and eastern lowlands) lie under the same and cooler Constant Threshold Region (-60^oC).
2. During normal years clouds and rain belt develop over the eastern escarpment or its adjoining highlands and move towards the western parts of the country providing more or less similar type of rainfall over the highlands, parts of the eastern escarpment and southwestern lowlands. This is in agreement with the fact that they lie under the same and relatively warmer Constant Threshold Region (CTR).

For the northern tip of the country and eastern lowlands –60^oC is found to be the optimum threshold in all months June to September. Over the highlands, southwestern lowland and parts of the eastern escarpment –40^oC in June, -50^oC in September and –30^oC in July and August are found to be the optimum threshold temperature. The linear relation between CCD and estimated rainfall is reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment. During the on-set (June) and cessation (September) of the summer rain the threshold for these regions is cooler than the thresholds within the season (i.e. July and August). This change in the threshold within the season can be explained in terms of weather producing systems as follows:

1. During the onset and cessation of the summer rain (i.e. June and September respectively) the rain-giving meteorological mechanisms may not be fully established and favourable to provide rain from relatively warmer threshold. Air must be lifted to a high altitude in order to be saturated and produce rain. Therefore, deep clouds with cooler threshold are required to provide rain; and
2. Within the season (July and August) rainfall occur from relatively warm cloud because of favourable rain-giving meteorological mechanisms. A slight ascent of the air leads to saturation, and therefore; relatively warmer threshold (-30^oC) provides rain.

The northern tip of the country and the eastern lowlands (coastal areas) lie under -60^oC Constant Threshold Region in all months June to September. This threshold is cooler than the threshold of the other constant threshold region (i.e. CTR that comprises the highlands, southwestern lowlands and parts of the eastern escarpment). The same and cooler threshold (-60^oC) over these climatic regions (i.e. northern tip of the country and the eastern lowlands) is also in agreement to the fact that both receive rainfall from deep storm that migrated to these regions from Yemen highlands. That means they get rainfall from deep cloud and from the same weather system (migrated storms). It should also be noted that there is lack of adequate rain gauge data over the eastern lowlands (i.e. coastal areas) and the northern tip of the country. For the CTR that comprises the eastern lowlands and northern tip of the country the determination of calibration coefficient and validation are not done for the following reasons:

1. except occasional rain, summer is mainly dry; and
2. during summer large number of events over these regions is no-rain and this resulted in zero median gauge rainfall. The zero median gauges obtained in turn made the calibration process difficult.

1. Evaluation of the Calibration Algorithm

Stability of the calibration may be tested by using the calibration derived from one year in subsequent years as well as by showing how far a given algorithm is applicable beyond the limits of the area containing the stations used for calibration (Milford, J.R. and Dugdale, G., 1990). However, in this analysis it was difficult to do such type of evaluation for the reason that there were only four years (1994-97) data available for this study and these data are totally used for the calibration. No independent data is left to do the validation.

The evaluation, though done not with an independent data set, indicated that there is a reasonable agreement between the satellite estimate and gauge value in all considered months (June to September). In June, July, August, and September over 76%, 67%, 60% and 83% of the stations respectively the gap between the satellite estimate and gauge value is less than 10mm – and this is reasonably good. Thus, the calibration algorithm works well. However, in some cases, the satellite estimate is lower than the gauge value and this may be explained climatologically as follows.

1. Some times during June and September there might be enough moisture and favourable low level winds to give rain and in this case rainfall may occur with a warmer threshold than the selected optimum thresholds (i.e. –40^oC for June and –50^oC for September). Such events may occur due to early onset or late cessation of the rain. Therefore, during those events the calibration algorithm gives an under-estimate.
2. Similarly, in July and August when there are strong rain-giving mechanisms continuous rainfall may occur from warmer cloud than the optimum threshold (-30^oC). This also leads to under-estimate of the calibration algorithm.

No particular climatic region is particularly influenced by the under-estimate, under-estimate occurred in different stations from different climatic regions. Therefore, it is difficult to identify a particular climatic region where the calibration algorithm is underestimating.

The validation, however, should be carriedout by the kriging method using independent data from the current and / or next summer season. The Kriging method is useful in the validation because it estimates errors related to the density of gauge network. Using the kriging method satellite estimate is plotted against gauge data with error bars. Therefore, whenever the satellite estimate lies within the error bar the estimate is reasonably good, otherwise not good.

1. Conclusions

In Eritrea rainfall is mainly convective and thus it is highly localized and has great temporal and spatial variability. Moreover, the sparse raingauge network is not uniformly distributed throughout the country. Therefore, in order to measure area rainfall on real time basis as accurately as possible there is a need to supplement gauge data using satellite estimates. The Eritrean Meteorological Service installed PDUS (Primary Data Users System) and has an access to half-hourly and hourly Meteosat images. However, so far no quantitative estimate of rainfall is introduced. The result of this study, therefore, will be important in introducing satellite based rainfall estimate and augmenting the raingauge data to obtain real-time area rainfall estimate.

The aim of this study is to discuss briefly various satellite-based rainfall estimation techniques that are relevant to Eritrea type of climate and to calibrate the TAMSAT technique for Eritrean summer rainfall particularly over summer-rain receiving parts of the country. Of many available satellite-based rainfall estimation techniques microwave, CPC, ORSTOM and TAMSAT are briefly discussed. These techniques are chosen because they are relevant to Eritrea type of climate. The microwave technique uses microwave sensors for estimating rainfall but it is not fully developed for real-time daily operational application. The ORSTOM technique uses ground surface temperature obtained from meteosat images and it is based on the inverse relationship of previous rainfall on ground surface temperature (Guillot, 1995). This technique is tested in west Africa and when combined with cold top cloud frequency technique the ORSTOM technique resulted in greater accuracy. However, the technique needs surface data and is calibrated against contemporaneous gauge data and this may make the technique difficult to implement in Eritrea at this stage. The CPC technique uses meteosat satellite data, real-time raingauge data, model analysis of wind and relative humidity and orographic features (Herman et al, 1997) to estimate rainfall both from cold and warm cloud. This technique is calibrated against contemporaneous data but is the only technique to estimate rainfall from warm cloud. The CPC technique may be important for Eritrea in estimating winter rainfall (that is mainly from warm cloud). It is also useful for estimating occasional warm cloud summer rainfall.

The TAMSAT technique is the one that is calibrated for summer rainfall of Eritrea in this study. It uses half-hourly or hourly infrared images and depends on the assumption that convective clouds are the main source of rain. There is a direct linear relation between cold cloud duration and estimated rainfall. This technique is the only technique that is entirely pre-calibrated against historical gauge data. Moreover, it is automated and easy for operational application.

Hourly Cold Cloud Duration (CCD) at different thresholds and gauge data from 1994 to 1997 are used in this study. Analysis was carried out in order to: determine the optimum threshold that discriminates rain from no-rain, delineate constant threshold regions, calculate calibration coefficient, and estimate rainfall using the regression equation. The result of the analysis indicated that during summer Eritrea falls into two Constant Threshold Regions (CTR): the first comprises the highlands, southwestern lowlands and parts of the eastern escarpment and the second comprises the northern tip of the country and eastern lowlands (coastal areas). Due to lack of gauge data no calibration was done for the northwestern lowlands. As discussed in section 5.1.2., the separation into two constant threshold regions (CTR) can be explained in terms of the following two different weather systems: the northern tip of the country and the eastern lowlands receive occasional rainfall from deep cloud with cooler threshold; while the highlands, southwestern lowlands and parts of the eastern escarpment obtain similar type of rainfall from relatively warmer clouds.

For the northern tip of the country and eastern lowlands –60^oC is found to be the optimum threshold in all months June to September. Over the highlands, southwestern lowland and parts of the eastern escarpment –40^oC in June, -50^oC in September and –30^oC in July and August are found to be the optimum threshold temperature. The linear relation between CCD and estimated rainfall is reasonably good over the highlands, southwestern lowlands and parts of the eastern escarpment. For the CTR that comprises the eastern lowlands and northern tip of the country the determination of calibration coefficient and validation are not done because during summer large number of events over these regions is no-rain and this resulted in zero median gauge rainfall.

Over the highlands, southwestern lowlands and parts of the eastern escarpment changes in threshold within the season are observed and this is explained in terms of the strength and variability of rain-giving meteorological mechanisms. When the mechanisms are strong and favourable they provide rain from relatively warmer threshold (e.g. July and August), otherwise deep ascent and hence deep cloud with cooler threshold is required (e.g. June and September).

The evaluation, though not done with an independent data set, indicated that there is a reasonable agreement between the satellite estimate and gauge value in all considered months (June to September). In June, July, August, and September over 76%, 67%, 60% and 83% of the stations respectively the gap between the satellite estimate and gauge value is less than 10mm – and this is reasonably good. However, sometimes the satellite estimate is lower than the gauge value and this underestimate in all months might be explained in terms of the strength of the rain-giving meteorological mechanisms and availability of moisture. When there is enough moisture and favourable low level winds then relatively slight ascent with warmer threshold than the optimum gives rain. In this case the calibration algorithm underestimates.

No particular climatic region is particularly influenced by the under-estimate, therefore, it is difficult to identify a particular climatic region where the calibration algorithm is underestimating.

Satellite based rainfall estimation gives a real-time broader overview of rainfall that is useful for agriculture, famine warning, hydrology, pest monitoring and erosion. More specifically, this information is useful to know whether the rain is sufficient for crop growth or not; and to predict river flow, erosion and potential locust outbreak areas. For Eritrea, which is located in semi-arid region near the Red Sea, these information is extremely useful.

Therefore, the results obtained from this study are useful for operational application in Eritrea. While being operational, however, continuous validation must be carriedout by the kiriging method using independent data from the current and / or next summer season.

Further improvement to the satellite based rainfall estimation is essential and highly recommended in order to increase the accuracy of the estimate. To that end, in collaboration with TAMSAT group and other relevant organisations it is essential to improve the estimate by:

1. using the TAMSAT technique to test CCD20 threshold which is not done in this study;
2. testing the CPC technique for the winter rainfall of Eritrea;
3. combining the TAMSAT technique with CPC for summer rainfall; and
4. establishing standardized and centralized gauge network in Eritrea that is a cornerstone for calibration and research work.

Barret, E.C. and D.W. Martin, (1981): The Use of Satellite Data in Rainfall Monitoring. Academic Press, london.

Barret, E.C and M.J. Beaumont, (1994): Satellite rainfall monitoring: an overview, in Remote Sensing Reviews, Goel, N.S and E.C. Barrett (eds.), pp 303-373. Harwood Academic Publications, USA.

Bonifacio, R. and Grimes, D.I.F, (1998): Rainfall Estimation Manual, Natural Resource Institutes

diplo, M., (1998): The influence of weather system on satellite rainfall estimation with application to river flow modeling.

ELIZABETH M. SHAW, 1994: Hydrology in Practice

Fantoli, Amilcare, (1966): Contributo alla Climatologia Dell’Altiplano Etiopico, Regione Eritrea.

Global Atmospheric Research Program (GARP) (1978): The West African Monsoon Experiment (WAMEX), GARP Publication Series No. 21.

Grimes, D.I.F., Milford, J.R and Dugdale G., (1993): The use of satellite rainfall estimates in hydrological modelling. Presented at the first international conference of the African Met. Soc. Nairobi, Kenya.

Guillot, B. (1995): Satellite et precipitations: Contraintes techniques et physiques, analyse de quelques methodes, problemes de recherche et de validation. Veille Climatique Satellitaire: 55, 27-58.

Habtemichael, A. and D.E. Pedgley, 1964: Spring Rainfall over Eritrea, Arch. Met. Geoph. Biokl, ser. A.23, 285-296

Herman, A., V.B. Kumar, P.A. Arkin and J.V. Kousky, (1997): Objectively determined 10-day African rainfall estimates created for famine early warning systems. Int. J. Rem. Sens.: 18, 2147-2159.

Houghton J.T and Taylor F.W., (1973): Remote sounding from artificial satellites and space probes of the atmospheres of the earth and the planets.

Kidder, S.Q. AND T.H. Vonder haar, (1995): Satellite Meteorology, an introduction. London: Academic Press.

Meteorological Map of Ethiopia, (1979), National Meteorological Services Agency, Ethiopia

Milford, J.R. and Dugdale G., (1990): Estimation of rainfall using geostationary satellite data, in Applications of remote Sensing in Agriculture, Steven, M.D. and J.A. Clark (eds.), pp 97-110. Butterworth, London.

Morland, J., D. Grimes, G. Dugdale and T. Hewison, (1997): The effect of the land surface on microwave rainfall estimates, in Proceedings of the 23^rd Annual Conference and Exhibition of the Remote Sensing Society, Reading, pp 493-498.

Pedgley, D.E. (1966): The Red Sea Convergence Zone: Weather 21, 350-358 and 394-406

Ramage, C.S. (1971): Monsoon Meteorology, Academic Press

Spencer, R.W., H.M. Goodman and R.E. Hood, (1989): Precipitation retrieval over land and ocean with SSMI: Identification and characteristics of the scattering signal. J.Atmos. And Oceanic Tech.: 6, 254-273.

Stanley Q. Kidder and Thomas H. Vonder Haar, (1995): An Introduction to Satellite Meteorology.

Tesfaye Haile, (1982): Mean general atmospheric circulation over Ethiopia and its vicinity, Internal Report. National Meteorological Services Agency, Addis Ababa, Ethiopia.

Twomey, S., H. Jacobowitz and H.B. Howell, (1967): Light Scattering by cloud layers. J.Atmos. Sc.: 24, 70-79

Van Buskirk R. and Araia A., (1994): Rainfall Statistics of Eritrea. Environmental Information Collection and Analysis Project - Dept. of Physics, University of Asmara.