ABSTRACT
We present results from a finite element heat balance model for an electric enjera (traditional Eritrean/Ethiopian bread) cooker, and compare its predictions with controlled cooking experiments. Enjera cooker efficiency is analyzed and the major factors affecting the energy intensity and efficiency of enjera production are presented. The greatest energy savings is attained by using enjera batter with a low water content (a savings method in widespread use in the Eritrean Highlands) and a cooking style that produces moist, thick to medium thick enjera. Major improvements in efficiency are also predicted if cooking plate thermal conductivity is improved. Modeling predicts that most of the efficiency improvements can be obtained by simply using modified clays of higher conductivity, rather than changing to metal cooking plates. The modeling in combination with the experimental results aid in formulating a series of actions to aid in the promotion and development of improved enjera cooking efficiency.
INTRODUCTION
In Eritrea and Ethiopia, the cooking of a traditional yeast- leavened flat bread (enjera or taita) is responsible for a majority of national energy consumption. Yet no literature exists in international journals reviewing or analyzing the efficiency or energy intensity of enjera production.
Enjera is a flat, moist yeast-leavened bread or pancake that is eaten by more that 30 million people in the horn of Africa. To make enjera one takes flour, mixes it with water in a ratio of approximately 1:1.5 and allows it to ferment at 20 - 25 degrees for three days. (shorter for higher temperatures.) Then one removes an upper layer of liquid fermention products and reactivates the yeast by adding hot water to the fermented dough in a ratio of approximately 1:2. The reactivated dough is then allowed to ferment for another 2 - 5 hours before cooking.
Enjera cookers (mogogos) come in several forms: electric, liquified petroleum gas (LPG) and traditional wood mogogos. This paper presents results for electric mogogos primarily.
For electric mogogos, the enjera batter (bHuQ) is poured onto a clay cooking plate at a thickness of 3 - 5 liters/mē of plate surface. The average power of the cooking plate is 12 - 13 kW/mē of plate surface for a 50% efficient cooker. Typical cooking plates are 55 cm. in diameter.
To analyze the major factors affecting electric mogogo efficiency, we developed a theoretical heat-balance model for mogogo operation.
HEAT BALANCE MODEL
The electric mogogo that we will analyze here consists of a clay cooking plate with an embedded, electric heating element. The cooking plate is supported from underneath by a flat galvanized iron sheet and on the sides by a cylindrical galvanized iron loop to which it is sealed with silicon glue mixed with clay.
Heat flows from the cooking plate to the different mogogo components and to the enjera. The primary paths of heat flow are the following:
- From the heating element to the plate surface where either heat is lost through convection and radiation, or heat is transferred to the enjera batter.
- From the cooking plate to the sides of the mogogo through conduction through the glue/clay connection and the sheet metal. Heat is then lost through radiation and convection from the sides.
- From the cooking plate through primitive dried mud insulation to the galvanized iron sheet metal bottom. Heat is then lost through radiation from the bottom.
- A minor heat-flow path is from the cooking plate surface to the lid cover and thence to the surrounding through convection and radiation.
We developed a simple numerical heat balance model that divides the cooking plate into N equally thick layers, and calculates the heat transfer between layers and through the cooking plate using the basic equation of conductive heat transfer. Meanwhile heat transfer at the plate surface is assumed to be via radiation and convection [Krieth & Bohn, p 276] to constant temperature surroundings when the plate is bare, and directly via conduction when enjera batter is present. When the batter is present, it is assumed that the batter stays at the boiling temperature of water in Asmara, Eritrea (92.4 deg. C), which fixes the temperature of the upper plate surface. There is also some accounting of heat transfer to the aluminum cover. The equations of radiative and convective heat transfer are used. For the convective heat transfer we used the correlation relations for convective transfer b/n the bottom and top surfaces of a horizontal enclosed space heated from below [Krieth & Bohn, p. 277]. We do not account for condensation heat transfer to the lid and assume that this has a minor effect on overall efficiency evaluation. The lid loses heat via radiation and convection, where the top of the lid is assumed to be a flat surface. The program provides two states for the lid: up with only heat loss to the surroundings, and down, with heat transfer from bare plate or enjera.
Heat transfer between the plate and the sides was assumed to flow through the 1 cm thick ring of clay/glue mixture (k =0.45) and thence to the galvanized iron sides which are assumed to be at constant temperature due to the high thermal conductivity of iron. The heat loss at the sides is through regular radiative heat transfer (emissivity of clean galvanized iron = 0.25), and through the convective heat transfer using the equations provided in [Krieth & Bohn, 1986, p 277].
The heat transfer to the bottom is assumed to be through a lumped bulk thermal conductivity coefficient (because it is difficult a-priori to estimate the thermal conductivity of irregular pieces of clay). Assuming purely radiative heat losses, losses from the bottom of the electric mogogo to the surrounding room are calculated. The average conductivity of the air and clay beneath the plate is calibrated with the observed temperature of the bottom of the mogogo.
A second parameter that is obtained via calibration with experiment is the total heat capacity of the cooking plate, which is obtained by matching the temperature increase during initial plate heat-up.
The standard parameters used in the numerical model for most simulation runs are summarized in the following table. All runs of the model use these parameters unless otherwise specified.
|
Thermal Parameters of the Mogogo |
Value |
Units |
|
Conductivity of Cooking Plate |
0.45 |
(W/mK) |
|
Cooking Plate Thickness |
0.020 |
(m) |
|
Distance b/n Plate Surface & Heating Coils |
0.014 |
(m) |
|
Cooking Plate Diameter |
0.55 |
(m) |
|
Heat Capacity of Cooking Plate |
11500 |
(J/K) |
|
Cooking Plate Upper Surface Emissivity |
0.98 |
|
|
Thickness of the Contact b/n Cooking Plate & Sides |
0.02 |
(m) |
|
Diameter of Plate-Sides Contact |
0.63 |
(m) |
|
Thermal Conductivity of Plate-Sides Contact |
0.45 |
(W/mK) |
|
Emissivity of Sides |
0.25 |
|
|
Heat Capacity of Sides |
562 |
(J/K) |
|
Thermal Resistance b/n Cooking Plate and Bottom |
4.0 |
(W/K) |
|
Emissivity of Bottom |
0.25 |
|
|
Heat Capacity of Bottom |
548 |
(J/K) |
|
Distance b/n Cooking Plate and Lid |
0.05 |
(m) |
|
Emissivity of the Lid |
0.11 |
|
|
Heat Capacity of Lid |
756 |
(J/K) |
where W = watts, J = Joules, m = meters, and K = degrees Kelvin.
The model is calculated with a simple explicit first order time stepping method, which was sufficiently efficient for the computing resources available.
EXPERIMENTAL METHODS & RESULTS
A series of 8 controlled cooking experiments were performed to evaluate the effect of different cooking styles, enjera thickness, and batter water content on cooking efficiency and energy intensity.
The energy used in cooking was defined as the energy necessary to raise the batter to a particular temperature, and evaporate the amount of water that was observed to be lost during the cooking process. For most cooking trials, the batter weight, enjera wet- weight, and enjera dry weight were measured.
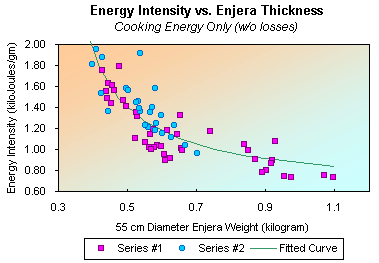
Figure 1
It is found that cooking thin enjeras can result in up to a 50% increase in the energy required per kilogram of enjera produced. While for thicker enjeras the energy intensity levels-off to a minimum value. The variations in the energy intensity of enjera production are dominated by the effect of the thickness of the enjera produced and are non-linear. The energy intensity of cooking (for a theoretically 100% efficient cooker) is illustrated in figure 1 . The figure shows the results for two series of experiments with different cooks and slightly different cooking styles. Cooking style variations include changes in the amount of time that the enjera is on the plate, and slightly different initial water content levels for the batter. The distribution of points is fit by a curve of the form:
y = a + b/(x-x0)
where a = 0.6 kJ/gm, x0 = 250 gm, b = 200 kJ, and x is the weight of a 55 cm enjera in grams. The root mean square deviation of the fitted curve with the experimental data is 0.17 kJ/gm. This deviation can be taken as the approximate variation in energy intensity produced by different cooking styles. The more efficient cooks will remove the enjera when it is relatively moist. The figure also demonstrates the dramatic increase in energy intensity for enjeras which are thinner than 550 grams per 55 cm diameter enjera (2.3 kilograms per square meter of plate surface). For thicker enjeras, the energy intensity levels off for thicknesses above 600 grams per 55 cm enjera (2.5 kg/m2) to an approximately constant level less than 1 kJ/gm. This implies that while some energy savings can be obtained by cooking very thick enjeras, the savings is marginal in comparison to medium-thick enjeras. Other factors such as the moistness of the enjera when removed from the cooking plate may have a larger impact on energy use.
Meanwhile, the cooker efficiency exhibited significant but small variations. The dominant effect appears to be that the efficiency becomes slightly higher when thinner enjeras with high- water-content batter is cooked. The observed efficiencies for the better-controlled experiments ranged from 43% for the thickest enjera to 55% for a series of very thin enjeras. For the thicker enjeras the efficiency was lower due to the lower energy requirements for cooking the enjera; with lower energy requirements, the fixed losses (plate heat storage and losses during cooking-plate heat-up) compose a larger fraction of total energy use. Furthermore, the thicker enjeras have poorer thermal conductivity within the enjera.
For the thicker enjeras, the total energy use per kilogram enjera (including both utilized energy and losses) was 1.7 kilojoules/gram for the thick 55 cm. diameter enjeras (4.1 kg/m2) while it was 70% higher or 2.9 kilojoules/gram for the thin enjeras (2.0 kg/m2). The total energy intensity for enjera production as a function of average enjera size is shown in figure 2 . Only one data point is shown per controlled cooking trial, since due to energy storage in the plate, efficiency can only be analyzed for an entire cooking session (and not for individual enjeras).
-
Figure 2
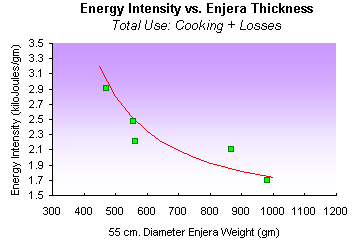
- Energy Intensity vs. Enjera Thickness: This figure illustrates the relationship between the amount of energy used to cook enjera and the thickness of the enjera. In this figure, the total energy intensity--including losses--is illustrated.
It should also be noted, that in actual practice, cooking efficiencies will be higher because for the controlled experiments the cooker was left on for the entire trial and until the final enjera was removed. It is standard practice in Eritrean households to briefly turn off the cooker during the cooking session, and to turn off the cooker 5-10 minutes before the cooking session is over. Cooking sessions where these practices were used exhibited efficiencies of nearly 60% rather than the 50% efficiencies observed in the experiments with continuous power use.
It is therefore concluded, that efficient enjera cooking styles (thicker enjera and power conservation during cooking) will use approximately half of the energy of less efficient cooking styles (very thin enjeras with continuous power use). From experimental trials alone, we can conclude that conservative cooking practices are a necessary and dominant factor in efficient energy use during enjera cooking. Such practices can reduce energy use by more than a factor of two.
COMPARISON OF MODEL AND EXPERIMENT
In order to compare the model with the experimental results. We run the model in a mode where the initial batter mass and pour- time is input, and the model predicts the mogogo efficiency, cooked enjera weights and mogogo component temperatures. Agreement between the model and the experiment will build confidence in using the model as a guide for design modifications that will increase efficiency.
Initial runs of the model with the standard parameter set mentioned in the previous section (and calculated from rough measurement of the a standard mogogo) slightly underestimate plate losses and overestimate plate heat retention for the mogogo used in our experiments. For comparison with experiments we reduce the plate heat capacity to 10000 J/K, and increase the effective plate diameter (for the sake of calculating heat losses from the plate surface) to 0.67 m. (this includes not only the plate, but also bottom rim of the mogogo around the plate). With these relatively small adjustments, the model simulates the mogogo operation quite well. For one of the cooking trials, the cooking plate surface temperature is measured in some detail. In order to attain agreement with experiment then, three parameters are adjusted: plate heat capacity, the thermal resistance between the bottom of the plate and the bottom of the cooker, and the effective plate diameter for calculating heat losses. All other model parameters are as listed above and are measured or taken from references on heat transfer.
Figure 3 shows a comparison between the plate surface temperature predicted by the model and the experimental measurements. The model fairly accurately predicts the initial plate heat up, the plate temperature rise between enjeras, and the plate cool-down. The detail with which the model can match the component temperatures in the mogogo provides some assurance that it can be used for analyzing new cooker designs.
-
Figure 3
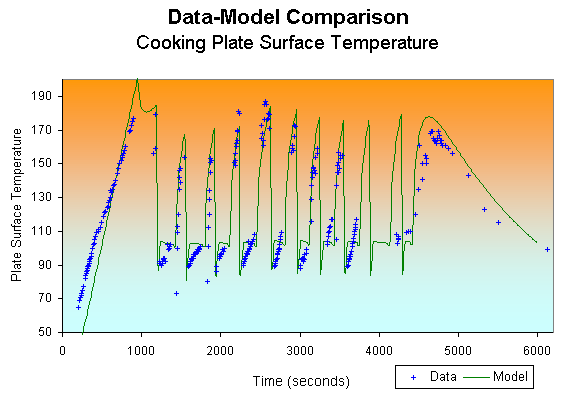
- Experiment--Model Comparison (Plate surface temperature): This figure compares the experimental data for plate surface temperature with the predictions of the simulation model.
We also compare the model predictions of cooker efficiency with those calculated from experiment:
|
Cooking Trial |
Experimental Efficiency |
Modeled Efficiency |
|
#1 |
42.2% |
46.9% |
|
#2 |
49.3% |
49.7% |
|
#3 |
46.9% |
53.4% |
|
#4 |
54.1% |
55.3% |
|
#5 |
44.3% |
47.6% |
The model show fairly good agreement with the experimentally measured efficiency values with some understandable deviations. One assumption of the model is that the enjera is in good thermal contact with the upper surface of the cooking plate. This is not true later in the cooking cycle when a dried bread layer forms on the bottom of the enjera and creates a thin insulating layer. This layer will decrease heat transfer to the enjera and decrease efficiency. In trial #3 for example, fairly thick dry enjera's were cooked while in trail #4 thin watery enjeras were baked. Where the water content of the batter is higher, the assumption of good thermal contact holds better, and there is good agreement with the model. Overall, the model overestimates efficiency and the RMS deviation between the model and the experimental efficiency values is 4%.
Figure 4 shows the agreement between the model predictions of enjera weights and the experimental values. Here the RMS difference between predicted and measured values is 40 gm, or 6% of the average enjera weight of 650 gm. Again the points which deviate most are those with the lowest final water content in the cooked bread.
-
Figure 4
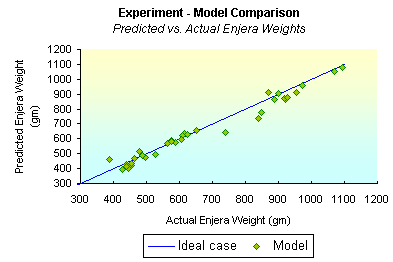
- Experiment--Model Comparison (predicted vs. actual enjera weights): This figure compares the measured enjera weights with those predicted by the model simulation. Given, the amount of batter, and the cooking time, the model predicted the enjera weight.
MODELING PREDICTIONS
Since the model has been largely verified by the experimental measurements, we can use the numerical cooker model to understand the different components of heat loss in the enjera cooker, and to provide guidance in improved designs for increased efficiency. For the simulations in this section, a reference plate heat capacity of 11500 J/K is used and the effective plate diameter is 0.55 m.
Efficiency & Loss Estimates:
Efficiency varies only slightly with the details of the cooking style and enjera size. Therefore in analyzing the general behavior of the mogogo efficiency as a function of different design parameters, we will run the simulation in a mode where equal-sized enjeras are cooked (from 850 gm of batter enjera with a cooked weight of 614 gm is produced). Generally parameters such as the input power, will be adjusted so that each enjera takes approximately 4 minutes to cook in the simulation (efficiency varies only slightly with input power). Then using this standard simulation mode, the parameters of the mogogo construction are varied to evaluate their effect on efficiency.
For a typical run of the calibrated mogogo simulation model we obtain the following breakdown of heat losses for a run which cooks nine enjeras in approximately one hour:
|
Breakdown of Component Heat Losses |
|
|
Heat used in cooking enjera |
53% |
|
Heat retained in plate after cooking |
23% |
|
Heat lost from bottom |
11% |
|
Heat lost from plate surface |
7% |
|
Heat lost from sides |
5% |
|
Heat lost through lid |
1% |
We see that in terms of efficiency, the biggest loss is through the heat retained in the plate, second, from the bottom and the third largest component is the heat loss from the plate surface. A significant portion is lost though the sides, and the thermal effect of the lid is effectively insignificant. Better insulation can aid in reducing heat losses through the bottom of the plate, and the heat retained within the plate can also be used for cooking other breads (most notably Quicha) on the plate after the enjera. Furthermore, the losses due to plate heat retention can be minimized by having longer cooking sessions. This is a very common practice in Eritrea where several families will use the same mogogo to reduce heat retention losses. This is especially important for more massive mogogos (such as the all clay wood mogogos) which have larger heat capacity. Meanwhile the reduction of the heat losses at the plate surface requires a reduction of plate surface temperature during the time that between enjeras when the plate is bare.
Factors Effecting Efficiency:
The simulation model indicates that the major factors effecting efficiency are: 1) Length of cooking session, 2) Thermal resistance of the cooking plate, and 3) Cooker insulation.
Length of Cooking Session:
Since such a large fraction of the heat supplied to the shorter cooking sessions remains stored in the cooking plate at the end of the session, increasing the total cooking energy use by cooking more enjeras will decrease these fixed losses. By simply increasing the length of cooking sessions one can increase the efficiency of the mogogo to as much as 69%. The simulation indicates that cooking sessions of 10, 20, 30, and 100 medium- sized enjeras should have efficiencies of 55%, 62%, 65% and 69% respectively because of the decreased relative size of the fixed losses.
Thermal Resistance and Capacity of Cooking Plate:
The existing design of the enjera cooking plate was developed because of its ability to regulate heat delivery to the enjera through heat storage and thermal resistance. Mostly two types of material have been used for mogogo plates, clay and iron. Iron plates have had mixed success in terms of cooking high quality enjera, but they have been used for enjera cooking in certain circumstances (specifically in the Eritrean expatriate communities in North America and Europe and by Eritrean liberation forces in the field).
The heat balance model provides an estimate of the internal heat distribution within the cooking plate which illustrates the effect of low plate conductivity and high heat capacity. Figure 5 shows the heat distribution within the plate in the upper centimeter right before the batter is poured, right after the batter is poured and right before the enjera is removed. What can be seen from this figure is that a relatively thin layer 6-8 mm thick is actively providing heat storage for the enjera cooking process, the rest of the plate is providing thermal resistance regulating the heat flow. The low conductivity results in high temperatures exceeding 300 degrees within the cooking plate.
-
Figure 5
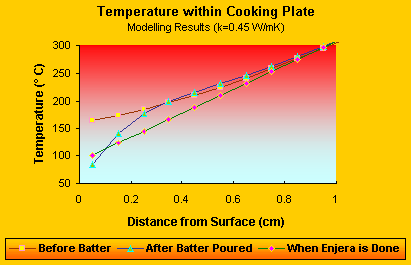
- Temperature within the Cooking Plate: This figure illustrates the temperature distribution within the cooking plate at different times.
We perform a series of other cooking simulations where we increase the thermal conductivity of the plate material, keeping the plate volumetric heat capacity and the average cooking time per enjera approximately constant. We then find the effect of increased plate thermal conductivity on cooker efficiency:
|
Thermal Condct. (W/mK) |
Power (W) |
Heat-up Temp. (deg C) |
Effic. |
Heat Retention |
|
0.45 |
2930 |
170 |
53% |
23% |
|
0.60 |
2930 |
170 |
58% |
21% |
|
1.20 |
2700 |
150 |
68% |
16% |
|
2.00 |
2600 |
140 |
73% |
14% |
|
10.0 |
2400 |
120 |
80% |
10% |
|
50.0 |
2300 |
110 |
81% |
9% |
(plate thickness = 2 cm)
In these simulations with increasing plate conductivity, the power is decreased and the initial plate heat-up temperature is decreased to compensate for the improved efficiency and more rapid heat delivery to the initial enjera resulting from the conductivity increase. Cooker efficiency is insensitive to these two parameters (a k=0.45 plate with power 2300 watts and heat-up temperature of 110 degree is only 56% efficient).
We can perform a similar series of simulations for varying plate thickness:
|
Plate Thickness (cm) |
Power (W) |
Heat-up Temp. (deg C) |
Effic. |
Heat Retention |
|
4.0 |
3500 |
170 |
31% |
43% |
|
3.0 |
3200 |
170 |
40% |
35% |
|
2.0 |
2930 |
170 |
53% |
23% |
|
1.5 |
2930 |
170 |
61% |
17% |
|
1.0 |
2930 |
170 |
69% |
10% |
|
0.5 |
2930 |
170 |
77% |
4% |
(plate conductivity = 0.45 W/mK)
We observe that theoretically, decreasing the thermal resistance of the plate by either increasing the bulk conductivity or reducing the plate thickness, contributes fairly dramatically to increased efficiency of the cooker. Furthermore, most of the efficiency gains are attained with only a mild decrease in the thermal resistance of the plate: For example by increasing the bulk conductivity of the plate material from 0.45 W/mK (the thermal conductivity of normal brick or ceramic) to 2.0 W/mK (the thermal conductivity of magnesite brick) efficiency can be improved from 53% to 73%. Simple clay modification procedures such as the addition of magnesium salts to the clay might be able to aid in producing a thermal conductivity increase in the plate.
Efficiency improves from decreased plate resistance primarily because the greater conductivity allows the cooking plate to operate at lower temperatures decreasing ancillary heat losses, plate heat-up time, and left-over heat. For a clay plate, most of the heat losses from the plate surface occur between enjeras and during initial plate warm-up when the plate surface reaches 170 degrees C. Meanwhile, for improved conductivity plates, the temperature of the plate surface between enjeras reaches only 140 and 110 degrees for plate conductivities of 2 to 50 W/mK respectively. Furthermore, the losses through the bottom are greatly influenced by the bottom temperature which decreases dramatically with increasing plate conductivity (current measured temperatures of the bottom can exceed 280 degrees C). Though the bottom losses could also be prevented through improved insulation. And approximately half of the efficiency gains for short cooking sessions are obtained by reducing the heat retained in the plate after cooking because of the lower internal temperatures of the plate during operation. The remaining significant heat loss is through the sides which can be decreased by having shorter sides or decreasing the thermal contact between the plate and the sides.
The effect of plate thermal resistance on cooker efficiency is illustrated in figure 6. Here the efficiency vs. the thermal resistance of the plate is shown (Plate thickness divided by bulk conductivity), for a set of simulations where plate thickness ranges from 3 to 0.5 centimeters, and bulk conductivity ranges from 0.3 W/mK to 50 W/mK. The square symbols represent simulations which cook nine medium enjeras, and the crosses represent simulations with 20 medium enjeras. The effect of the plate heat capacity and other factors on the cooking efficiency produces some scatter in the calculated efficiencies, but the plate resistance remains dominant. The collection of points can be fit by a regression line: e = 81 - 508 R, where R is the thermal resistance of the plate in units of Km2/W, and e is the efficiency in percent. It should be noted that while the precise impact of plate conductivity on the efficiency of other cookers is as yet unknown, the general effect will be the same and decreased plate thermal resistance will be probably a primary method for increasing efficiency in all cooker types.
-
Figure 6
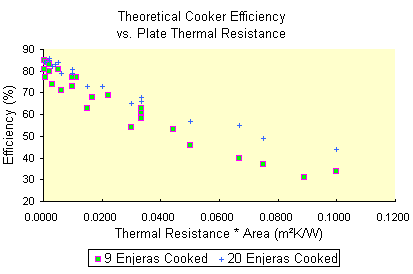
- Cooker Efficiency vs. Cooking Plate Thermal Resistence: This figure shows how the efficiency of a cooker increases with decreasing thermal resistance of the cooking plate. The illustrated results are predictions of the simulation model.
Insulation:
Only moderate efficiency improvements are attained through increased insulation. While 16% of heat losses from the standard run occur through the bottom and the sides, increased insulation increases internal plate temperatures and losses due to heat retention in the plate. Furthermore, the increased temperatures produced by greater insulation allows for greater heat losses through other paths. It is found that approximately a 5% - 10% efficiency improvement can be attained through such insulation. We perform simulations where the thermal resistance between the plate and the sides, and the plate and the bottom are increased by a factor of four, and compare these to the non-insulated case:
|
Insulated/Non- insulated |
# of Enj. |
Efficiency |
Side & Bott. Loss |
Heat Ret. |
|
Non-Insulated |
9 |
53% |
16% |
23% |
|
Insulated |
9 |
59% |
4% |
29% |
|
Non-Insulated |
20 |
62% |
17% |
12% |
|
Insulated |
20 |
70% |
4% |
15% |
Since insulation is quite inexpensive, this should be included in improved designs, but greater levels of improvement will also require other measures such as decreasing the thermal resistance of the plate.
Power Delivery Characteristics:
Another interesting feature of the simulation is the power delivery to the enjera immediately after the batter is poured. This power delivery function (specifically the big spike in power initially delivered to the batter) is a necessary requirement for the cooking of socially acceptable enjeras. Good quality enjera must have a large number of `eyes' or bubbles which give the bread its light spongy character. Without such bubbles, the bread will not properly absorb the sauces which are traditionally poured on top of the enjera and eaten with it. But the formation of proper or `good' enjera requires a specific rate of initial power delivery. Too little power delivery will not properly boil the water in the batter to produce the bubbles, while too much power will create uneven boiling and a thin cooked layer that deminishes proper conduction of heat to the rest of the batter. We do not yet know the details of the power delivery requirements but can provide a model comparison of power delivery difference for standard ceramic, improved-conductivity ceramic and metal plates.
-
Figure 7
- Initial Energy Delivery to Enjera: This figure illustrates ...
Figure 7 shows the different initial energy delivery curves for a standard ceramic, improved ceramic, and iron plate respectively in the initial minute of enjera cooking. The iron plate is given a high heat capacity (of 23000 J/K) so that it does not overheat in the times between enjeras. And the curves are taken for the third enjera in the series so that the heating cycle in the plate has had a chance to settle down (rather than using the energy accumulated during initial plate heat-up). It is seen that one consequence of the increased thermal conductivity is the larger initial energy delivery to the enjera. Eritrean mogogo manufacturers who have experimented with metal mogogo plates have commented that without thermostatic regulation, the excess power delivery from the plate badly cooks certain types of enjera.
CONCLUSIONS AND RECOMMENDATIONS
Detailed study of the thermodynamics of the electric mogogo and enjera cooking yields a quantitative estimate of the efficacy of different energy savings strategies. In order of priority they include the following:
|
Measure |
Energy Savings |
|
Cooking Thick/moist enjera |
20%-50% |
|
Long/shared cooking sessions |
10%-15% |
|
Greater plate conductivity |
10%-20% |
|
Increased insulation |
5%-10% |
|
Combined measures |
40%-70% |
Specific activities can be undertaken to attain these improvements in practice. Some of these measures are as follows:
- Education and Publicity on Efficient Cooking Practices.
- Testing and Possible Promotion of High-conductivity Clay Plates.
- Testing of Iron Plate Designs (with possible thermostatic control).
- Promotion of Increased Insulation.
Education and publicity activities on can include newspaper articles, radio, and television programs discussing energy use in enjera cooking and encouraging the most effective energy savings strategies which are already in use in Eritrea. This will increase the fraction of people using these strategies and help increase the level of energy savings. Such activities can be begun immediately.
In order to increase the conductivity of the plate and (which should benefit mogogo efficiency in all mogogo types), two activities need to be pursued. The first is the investigation of higher conductivity clays and their promotion once found. Higher conductivity clays include those such as Magnesite clays which possibly can be formed through the addition of magnesium salts to regular clays. Magnesium salts are currently a discarded by- product of sodium salt production in the Eritrean city of Massawa. Furthermore, the thermal conductivity of ceramics increases with increasing firing temperature and modifications in the process of forming the clay plates may aid in increasing their thermal conductivity. The second necessary activity is the testing of iron plate designs (perhaps with thermostatic control). The iron plate designs because of the very high plate conductivity will provide the most efficient power delivery to the enjera, but also may present problems of heat delivery control.
Insulation while providing only moderate improvement can still have a significant impact on mogogo efficiency. Such insulation is currently not easily available in Eritrea, but this problem can possibly be resolved by contacting building materials importers and making arrangements for them to import fiberglass on a regular basis. This then would enable manufacurers in a wide range of industries to increase the energy efficiency of their devices and products.
Enjera cooking is the dominant energy consumption activity in Eritrea and Ethiopia. Combined energy conservation measures can reduce energy consumption 40% to 70% for this use. Congnizant of the environmental and economic consequences of inefficient energy use, this study outlines those measures which can be promoted to obtain the greatest energy savings in Eritrean and Ethiopian households.
Acknowledgements:
The authors would like to acknowledge support for this research from primarily the Department of Energy, with assistance from the State Government of Lower Saxony, Germany, the University of Asmara, Asmara, Eritrea, and the Eritrea Technical Exchange, San Fransisco, California, U.S.A. Furthermore, the research was kindly assisted by Gabriela Fesehatsien, Ghenet Menghisteab, and Mebrak Goitom.
REFERENCES
Baldwin, S. F., Biomass stoves, engineering design, development, and dissemination, PU/CEES Report No. 224, Princeton University, The Center for Energy and Environmental Studies, Princeton, N.J., December 1986.
Incropera, F. P., and DeWitt, D. P., Introduction to Heat Transfer, John Wiley & Sons Inc., New York, 1985.
Kreith, F., and Bohn, M. S., Principles of Heat Transfer, Fourth Edition, Harper & Row, New York, 1986